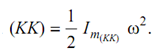Kinetic Energy of Translation/Rotation:

If (V) is the linear velocity of a body of mass (m), Kinetic-Energy of translation is the amount of work it has to give up before this is brought to rest. Kinetic Energy of the body, at rest, is obviously zero. Assume that a retarding force (R) Newton is applied to the body to bring its velocity from (V) m/sec to zero during which it travels a linear distance (s) metres,

∴ KE of the body = R × s N-m.

As the motion has uniform retardation say (- a), we have the equation of motion as

(V ₂)²  =( V ₁)² - 2 a s

where, ultimate velocity, V₂  = 0

primary velocity , V₁ = V

∴ 0 = V ²  - 2 a s

∴ Retardation, a = V² /2 s

Therefore the force of resistance (R) is given by

R = m × a = mV ²/2s

WD by R through distance

= R × s = mV ²/2s

Therefore, KE of translation = R × s = mV ²/2s

or,        = WV ² / 2 g

Here, W is the weight of the body of mass (m).

In case of angular motion of the body of mass (m) around any given axis (KK), if ω is the angular velocity of the body is radians/sec and r_g (KK) is the radius of gyration of body around its axis of rotation (KK), then mass-moment of Inertia (I_m) of the body about axis

(KK) is given by

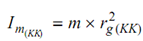
Angular retardation, α = ω²/2 θ , where θ is the angular distance travelled before coming to rest under a couple of resistance

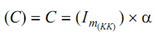
∴          WD by couple (C) = C × θ

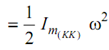
∴          Kinetic energy of rotation around axis of rotation (KK)