Wind Forces on Chimneys:

Having seen the stress distribution for any wall subjected to wind forces, let us assume the effect of wind forces on all of chimneys.

Figure illustrated a cylindrical chimney of height H, external diameters D, internal diameter d, subjected to horizontal wind pressure p as illustrated.

If γ refer to the unit weight of the masonry structure, direct stress because of the weight of the structure on its base f₀ = γ H.

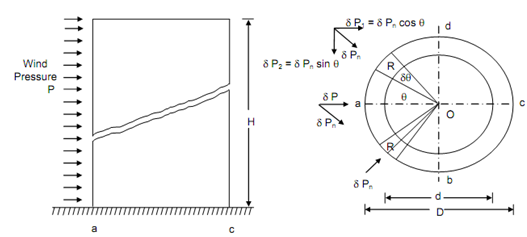
           (a) Elevation                                             (b) Cross-section

Figure

Assume a small strip of width R δθ, subtending an angle δθ at the centre and making an angle θ with the axis ac of the section,

δP = Wind force reaching the small strip

     = p × R δ θ × H cos θ 

= p H R δ θ cos θ

Element of the force normal to the strip,

δ Pn  = δ P cos θ

= p H R cos θ × δ θ × cos θ

= p H R cos²  θ δ θ

Horizontal component of

δ P_n  = δ P₁ = δ P_n  cos θ

  = p H R cos³  θ δ θ

Another horizontal component of

δ P_n  = δ P₂  = δ P_n  sin θ

Whereas summing up, this component gets cancelled out when we let a strip in the other quadrant as illustrated in Figure , while the components of P_n cos θ are added up.

∴          Net force in the direction X-X = 2δ P_n  cos θ

                                                          = 2 p H  R cos³  θ δ θ

Integrating over the entire exposed surface, from θ = 0^o to 90^o.

Total wind force

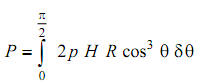
= p DH × (2 /3)= k × p DH

where, k = Coefficient of wind resistance, and

DH = Projected area of the curved surface.

BM because of wind force, M = PH /2

= p DH(2/3) × (H/2)

= p DH² /3

Section modulus, Z = π (D⁴  - d ⁴ ) /32 D

Bending stress, f _b =± M/ Z

Once you determine the bending stress, the extreme fibre stresses might be obtained by summing up with the direct stress due to self weight.