Logrolling:

Logrolling means vote trading. Individual X supports the preference of Y in one case provided that Y supports the preference of X in the other case. It is illustrated in the following example.
 
Suppose the Government is making expenditure in the Education sector and also in the Health sector. Education is explained by the size of school (S) and Health is explained by the size of Hospital (H).
 
Let H1, H2, H3 represent low size, medium size  and big size of the hospital. The preference patterns of individual X, Y and Z is given as follows: 
  X:      H₁ >  H₂  >  H₃
  Y:      H₂ >  H₃  >  H₁
  Z:      H₃ >  H₂ >  H₁
Applying majority rule the group choice will be  H₁ >  H₂  >  H₃ . Similarly, for school sizes, the preferences are as follows:

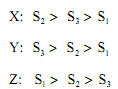
Applying majority rule the group choice will be 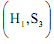It is obvious that following majority rule the final outcome will be   in the  group choice, i.e. point M in Figure. Point X, Y and Z represent best position for individuals X, Y ad Z respectively on the basis of their preferences for (H and S). 

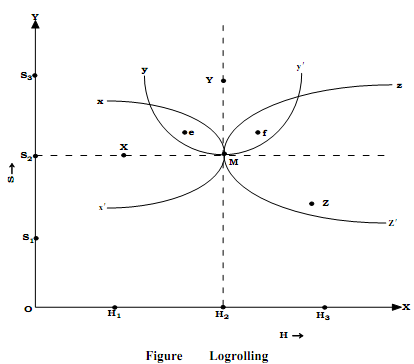
XX′ YY′ and ZZ' are indifference contours for individual X, Y and Z respectively. 

The closer the contour  XX′  is towards the point X in Figure the higher will be the level of welfare enjoyed by individual X.  Similarly are for individuals Y and Z. Suppose  there is vote trading between individual X and Y.  Y supports the preference of X for H and in exchange X supports the preference of Y for S.  This gives the group choice finally  according to the majority rule and considered to rest on point 'e' in Figure.

If again there is logrolling between individual Z and Y, Z supports the preference of Y for S and in exchange Y supports the preference of Z for H.  This leads to final group choice 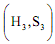  and considered to rest on point 'f' in figure.

Point 'e' and 'f' are different and it leads towards cyclic voting for H.  Therefore in this case logrolling fails to derive the group choice. For the success of logrolling an individual has to go for vote trading only with another individual, not with more than one individual simultaneously.