Tiebout Model:

Assumptions:

1) 'Consumer-voters' will move to jurisdictions that meet their particular preferences.

2) It is assumed that they have complete information regarding the local taxes and provisions of local pubic goods.

3) They will be sought by those jurisdictions with less than an optimal number of residents for its chosen expenditure pattern.

4) There is costless mobility in the sense that job search costs, transportation costs etc. are very low relative to the gains out of migration.

5) The movement of individuals from one locality to another should not cause externality in the form of added congestion adversely affecting others' utility in the destination location. 

Mechanism:

For a welfare maximizing equilibrium, the Tiebout mechanism must create a situation whereby it is impossible for any individual (as well as for the localities) to increase utility as a result of changing communities.

Assume that individuals migrate between localities until the benefit they derive from being resident in one locality is equal to the  benefit they derive from being in another.

If marginal benefit or utility derived from entering into locality X is denoted by MBx and marginal benefit from entering into Y is MBy, then individual (as well as social) equilibrium occurs where,

MB_x  = MB_y

As this condition gets satisfied, there is no further movement across the localities X and Y. Thus, we have social stability as well.
However, when an individual moves to a region, 'congestion costs' may be added to already crowded facilities. If MCx and MCy represent marginal congestion costs of adding one more person to regions X and Y respectively, then individual welfare maximum requires that net individual benefits (including the direct individual benefits / losses acquired through migration and also the cost of 'congestion externality' due to migration) even after movement across the two regions are equal:

MB_x  - MC_x  = MB_y  - MC_y

Here, as an individual is assumed to migrate from region Y to region X, extent of congestion increases in X and that is reduced in Y.  With internalization of these externalities the optimum is reached. Thus, a process of migration goes on until the net marginal individual gains (including the congestion cost) from entering into regions X and Y i.e. MB_x  - MC_x  and MB_y  - MC_y  respectively get equalized.

This process of migration could be made more realistic by incorporating tax to finance local public expenditure. As a result, the benefit of one more resident in X is MB_x  - t_x  where t_x  is the tax paid by the marginal immigrant. Similarly, the corresponding value for  region Y is TB_y  - t_y . Ignoring problems of congestion and following the above-mentioned procedure it is argued that an individual  welfare optimum requires:

TB_x - t_x = TB_y - t_y

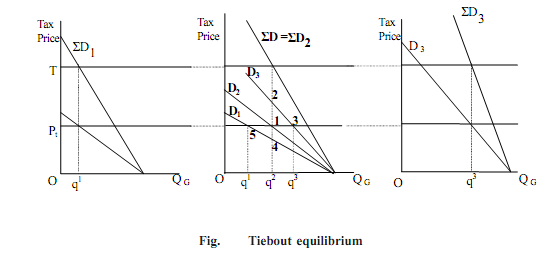
Free migration will result in an optimum only if t_x  = t_y , that is, if the total tax bill for marginal individual is the same in the two  regions. A priori, there is no reason to expect that the tax bill per person will be the same in both regions. However, a question could be raised against this criticism. If there were a divergence in tax bills, then, other things equal, there would be a preference to reside  in the locality where the tax bill is lower. If one area were to turn out to be a tax haven, property and house prices would rise  (capitalizing the favourable tax bill) in this area, so reducing its MB. Holcombe illustrates the Tiebout equilibrium using a diagram like  Figure (below). In part (b) of the figure the vertical sum of three individuals with different demand curves (D₁ , D₂  and D₃ ) for a  local public good G is ΣD. With a marginal cost of provision of G equal to OT and equal tax shares, the equilibrium quantity (as ΣD = MC) is Oq² . For this outcome for individual 1, whose demand curve is D₁ , there is a welfare loss from over-provision of triangle 145.  For individual 3 the welfare loss from under-provision is triangle 123. If there are competing local jurisdictions, individual 1 can 'exit' to a community of like-minded individuals, and similarly for individual 3. In an ideal outcome there would be three communities with  equilibrium as is parts (a), (b) and (c) of the figure. With (three) identical individuals each enjoying a situation where their demand equals OP^t , there are no welfare loss triangles. In each community there is a different level of provision of local public goods Oq¹ , Oq²  and Oq³ . Given fiscal migration, welfare losses from allocatively different outcomes from some individuals' equilibrium quantities  can be avoided.