Proof of Expected Utility Property:

Suppose that  the rational preference relation 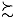on the space of  lotteries L satisfies the  continuity  and  independence  axioms. Then 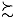admits  a utility representation of the expected utility form. That  is, we can assign a number u, to  each outcome n = 1.. . ,N  in  such a manner that for any  two lotteries L = 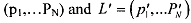,  we have L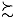L'  if and only if

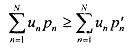
Proof: (Taken rnoslly  from Aulor, 2004) Assume that there are best and worst lotteries in  L,  and  L

1)  If 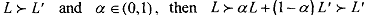 (due  to  the indegendence axiom)

2)

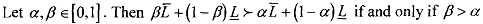
3) For any  L ∈ L,  there  is a unique  aL such that 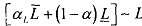  .  (due to continuity axiom)

4) The function  U: L -> R that assigns  u  (L)  = a,  for  all  L ∈ L represents the preference relation 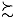. From (3) above for any two lotteries we have

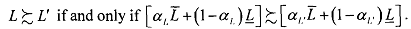
5) The utility function U(.)  that assigns U(L)  =  a, for all  L G L  is linear and therefore has the expected utility form. We want  to  show  that for  any  L,  L'  E  L,  and  ~[0,1],  we  have

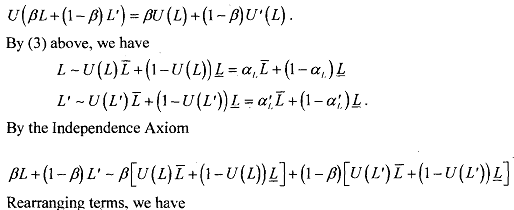
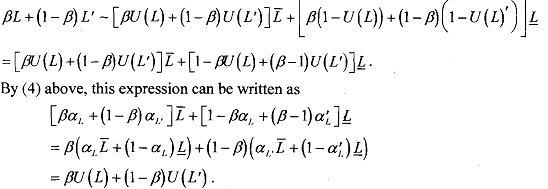
So, we have established that a utility function satisfying the continuity and the Independence Axiom, has the expected utility property:

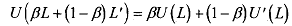
In brief, we can say that, a person who has vNM expected utility preferences over lotteries will act  as  if  she  is maximising  expected utility -  a weighted average of utilities of each state, weighted by  their probabilities. To  use  this model,  we  need  a  utility  function that bundles into  an  ordinal utility  ranking.  Note  that such functions are defined up  to  an  affine  (i-e., positive linear) transformation. This means  they  are required to have more structure (i.e.,  are more restrictive) than standard consumer utility functions, which are only defined up to a monotone transformation