Virus symmetry

The capsids of virions tend to have one of two symmetries – helical or icosahedral (geo- metric). Helical symmetry can be loosely described as having a ‘spiral staircase’ structure, with an obvious axis down the center of the helix. The protein subunits of a helical capsid mirror the helical turns of the nucleic acid. Viruses with a helical capsid structure include measles, rabies, and influenza. Some helical viruses appear to be ‘open-ended’ while others are enclosed structures where the protein subunits seal the capsid at one or both ends. Many viruses have geometric (sometimes called cuboid) symmetry, tending towards a spherical shape. Obtaining a true sphere is not possible although the protein subunits come together to produce a geometric structure that is very close to being spherical. These virus capsids are always fully closed and are usually based on an icosahedron. A regular icosahedron forms from the assembly of identical subunits arranged to give 20 equilateral triangular faces, 30 edges and 12 vertices (corners). The structure exhibits multiple symmetries, with 2-fold axes running along each edge, 3-fold axes centered in each triangular face, and 5-fold axes at each corner. The minimum number of capsomers required to construct an icosahedron is 12, each composed of five identical subunits forming the adjoining corners of the capsid structure. Many viruses have more than 12; Adenoviruses display such an arrangement as illustrated in Figure.

Adenoviruses have 12 projecting fibers, one present at each vertex, making this capsid highly distinguishable from that of other viruses. The maturation and assembly of icosahedral viruses is very complex and much of what happens is unknown. Usually icosahedral capsids form via a complex but structured array of molecular-assembly procedures that eventually give rise to the mature capsid. These may be self-assembly processes or they may involve virus non- structural proteins, acting as temporary scaffolding proteins, which do not form part of the mature capsid.

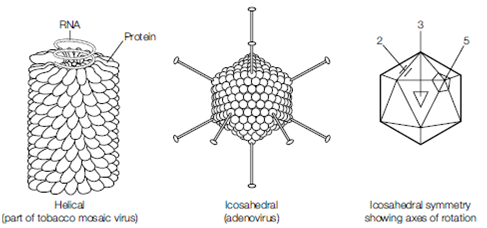
                         Figure:  Diagrammatic representation of helical and  icosahedral symmetry.