Vibration of Two Degree of Freedom Systems:

In the end also we had discussed free vibrations of a three rotor system that is a two degree of freedom system. A two degree of freedom system contains two natural frequencies as well as the two modes of vibration.

Vibration of a Spring Mass System

A spring mass system is illustrated in Figure 19(i). The free body diagrams the two masses are illustrated in Figure 19(ii). The force equations may be written as:

m₁  ? ₁  + k₁ x₁  + k₂  ( x₁  - x₂ ) = 0

m₂  ? ₂  + k₂  ( x₂  - x₁ ) + k₃ x₂  = 0

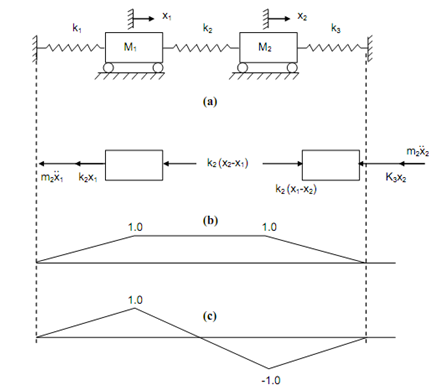
 These are the differential equations for spring mass system.

Let x₁  = X₁  cos wt

and x₂  = X₂  cos wt

On putting for x₁ and x₂ in Equation (70) and on simplify the following is attained.

(k₁ + k₂ - m₁ w²) X₁ - K₂ X ₂ = 0

 And    - k₂ X₁ + (k₂ + k₃ - m₂ w²) X ₂  = 0

 For a exclusive solution of the homogeneous equation

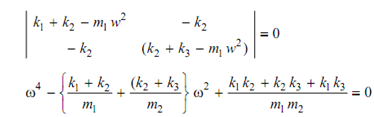
To simplify the solution, Consider k₁  = k₂  = k₂ and m₁  = m₂ .

∴          ω⁴ -( 4k/m) ω² + 3k₂/m²  = 0

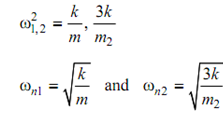
For measuring mode of vibration, any one of the equations of Equation (71) may be utilized.

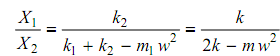
For

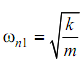
Let   X₁ = 1.0

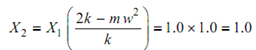
For

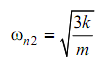
Let X₁ = 1.0

   X ₂ = 1.0(( 2k - 3k )/ k)= - 1.0

These modes have been plotted in Figure 19(iii).