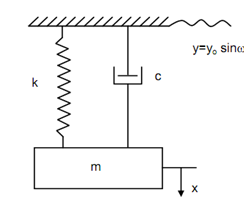
Vibration Due To the Base Excitation:

A spring mass system is illustrated in Figure 1 in which the base of suspension is vibrating along the function.

 y = y₀  sin ωt               -------------- (1)

The equation of forces might be written as following

m x'  + c ( x'  - y' ) + k ( x - y) = 0

or            m x'' + cx'+ k x = c y'  + k y                                  ---------- (2)

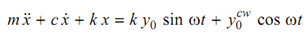
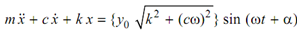           ---------(3)

Here

α= tan ^-1  ( cω /k)                          -------- (4)

α is phase angle among base excitation and force.

Assume

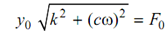
∴             mx''  + cx'  + k x = F₀  sin (ωt + α)               ------------(5)

As described in the last unit, steady state the solution of the above equation is given by

x = X sin (ωt + α - φ)

φ is phase angle among force F₀ and displacement here

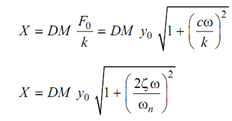   . . . (6)

The angle (α - φ) is the phase difference among the base excitation and vibration of mass 'm'.                                              

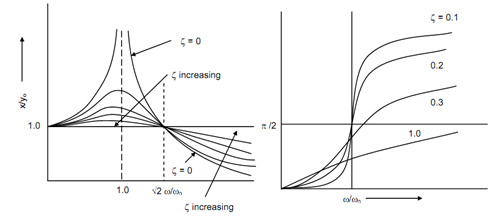
The response of mass 'm' and phase angle have been plotted in Figure 2. The following points might be noted down.

 (i) The response is either equivalent to the excitation or greater than it for ω/ ωn ≤ 2 .

 (ii) At ω/ ω_n = 1 , the response is extremely large for small amount of damping.

 (iii) For ω/ ω_n > , the response is smaller than the excitation and damping has very little influence. Damping enhances response.