Transmissibility and Vibration Isolation:
The transmissibility refers to the ratio of maximum force transmitted to the maximum impressed force.
From Equation (15)
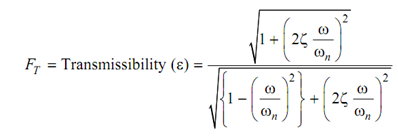
Graphs may be plotted among transmissibility and frequency ratio. Figure 7 illustrated these graphs. This may be noted down that all of the curves pass through (0, 1) & (2, 1). The transmissibility is more than 1 for frequency ration 0 < ω/ ωn <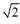
. Throughout this range of frequencies damping is most effectual in dropping the transmissibility. For frequency ratio more than 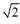transmissibility is always < 1. For this frequency range damping enhances transmissibility. The frequency range 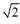< ω /ωn < α is very good for maintain transmissibility low however damping must be as low as possible.
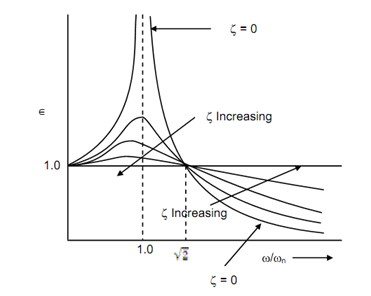
This is highly wanted for design of machine mounts so that vibration is exactly isolated. The unbalanced force is a machine is transmitted to the ground like a shaking force through its mount on the foundation. Hence, appropriate isolators must be used to drop or eliminate shaking forces transmitted to the ground. Such a design is known as active isolation design. If machine mounts are designed to drop or eliminate three motions being transmitted from the ground to the machine, this is known as passive isolation design.
Letting Figure 7, the following points might kept in mind :
(i) For ω>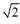ωn , output is smaller than the input. Hence, for effective isolation the natural frequency of the system must be less than 0.707 times the operational speed or harmonic frequency i.e. to be isolated.
(ii) For ω>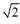ωn , damping enhance transmissibility therefore the damping must be kept as low as possible.
(iii) If ω<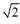ωn , more and more damping must be utilized to maintain transmissibility as low as possible.