Solution of Differential Equation:

The differential eq of single degree freedom undamped system is given by following

                   m x' + kx = 0

or         x' =   (k /m)x = 0                . . . (7)

While coefficient of acceleration term is unity, the underroot of coefficient of x is equivalent to the natural circular frequency, that means 'w_n'

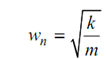                             . . . (8)

Hence, Eq. (7) becomes like this

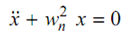                  . . . (9)

The eq is satisfied by functions sin w_n t and cos w_n t. So, solution of

Equation ( 9) may be written as

            x = A sin w_n t + B cos w_n t        . . . (10)

Here A and B are constants. These constants can be estimated from primary conditions. The system illustrated in Figure 2(i) might be disturbed in two  following ways :

 (i) by pulling mass by distance 'X', and

 (ii) by hitting mass by means of a primary moving object having a velocity say 'V'.

Letting (a) case

 t = 0,  x = X   and    x'= 0

∴ X = B         and          A = 0

∴ x = X cos w_n t   . . . (11)

Letting (b) case

t = 0,         x = 0 and         x' = V

B = 0   and A = V/ w_n

∴ x  = V/ w_n sin w_n t           . . . (12)