Energy Method:

This method is applicable to the conservative systems only. In conservative systems entire energy remains constant. While a mechanical system is in motion, the entire energy of the system is partially kinetic and partially potential (elastic strain energy). The kinetic energy is because of the velocity (x ) and mass (m) and potential energy is because of spring stiffness and relative movement among the two ends of the spring.

              Energy (E) = T + U = constant (C)

here  T = Kinetic energy of the system,

U = Elastic strain energy.

As total energy remains constant

∴          dE /dt= 0   or d/dt  (T + U ) = 0

            T =( 1/2 ) m (x')

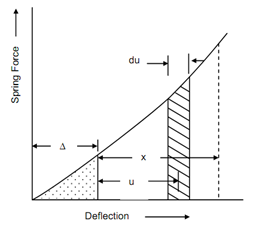
  Figure 4

The potential energy of the system has two following points:

(i) loss/gain in PE of mass, and

(ii) strain energy of spring.

Let an infinitesimal element du at x = u.

From Figure 4

Spring force (F_u ) = k (u + Δ)

Work done dW = k (u + Δ) × du

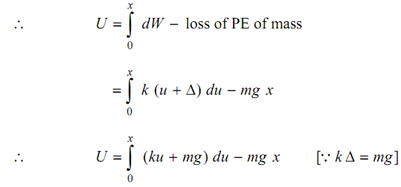
                   or  U = ½ (kx² ) + mg x - mg x

or                 U = ½  kx²                                    . . . (5)

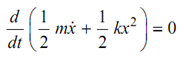
∴          (½ m × 2 x' × x' ) +( ½ k × 2x )+ x'= 0

or         mx'+ kx = 0

This is the similar equation as we obtained earlier.