PEXE Method

The distribution function called Piecewise Exponential Estimator was proposed by Kitchin (1980). In a data of size n, if t₁, t₂, . . . , t_i are observed failure times and t_i1, t_i2, . . . , t_im are suspended data between two successive failure times, then the failure rate estimation is given by,

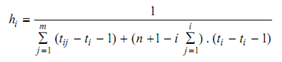
The survival function is given by,

R (t) = exp (- h₁t)     0 ≤ t ≤ t₁

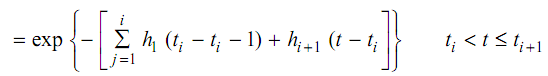
 In this method, constant failure rate is fitted to each interval. The exponential survival functions are pieced together to form piecewise exponential estimator. This is a continuous function. In order to construct the TTT plot from PEXE an estimate of survival function after time t_n must be made. If there are suspensions after last failure, then final TTT can be obtained using Equation. If there is evidence that failure distribution is increasing failure rate (IFR) class, then Weibull distribution can be assumed and the final term of TTT_{n + 1} can be evaluated using the expression.

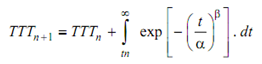
Where α (scale) and β (shape) are parameters of Weibull distribution. The method of evaluation of second term in equation is described in next section. [The PEXE can be seen as a generalization of the Nelson estimator in its original form, i.e. without any suspensions, the PEXE is equal to the Nelson estimator].

Precisely, Survival function is

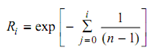
and S_i is

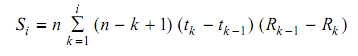
The scaled TTT, φ_i is equal to Si / S_{n +1}, where S_{n + 1} is given by

S_{n +1 =} S_n + (α / β).   (t_n/α) . Exp [- (t_n / α)^β]

And α and β are ML estimates of Weibull distribution.