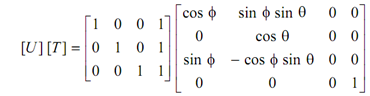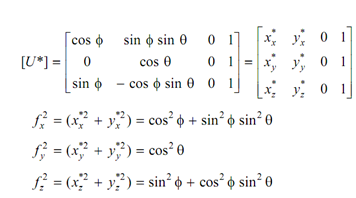Transformation position vectors:

Foreshortening ratios are attained by applying concatenated transformation matrix T to the unit vector along with principal axes (axis or edge originally parallel to one of the x, y or z coordinate axes

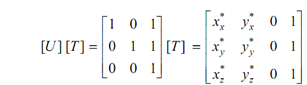
U is unit matrix along with untransformed x, y & z-axes. Foreshortening Factors along projected principal axes are following

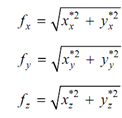
Let an object rotated by an angle φ around y-axis, by an angle θ around x-axis and then parallel projection on Z = 0 plane. In that case transformation matrix T is given by

                                      [T ] = [ R_y ] [ R_x ] [ P_x ]

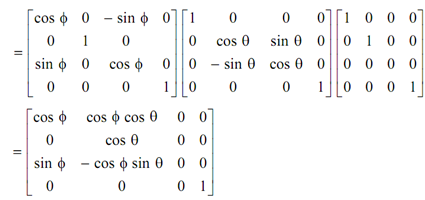
Transformation position vectors may be obtained by multiplying original position