Vibration of Shaft/Beam due to Its Own Mass:

There are two approaches to deal along this case. One of is easier but one assumption is taken in analysis that is consistent to the practical situation. It is called Approximate Method and the other one contains no such assumption is required but boundary conditions are considered is known as the Exact Method.

Approximate Method

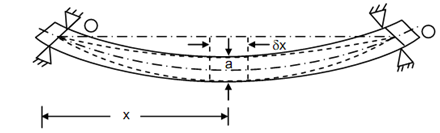
Assume m = Mass of the shaft/beam per unit length,

l = Length of the shaft,

y = Displacement at distance x due to its own static load,

a = Amplitude of vibration at distance x,

y_e = Displacement at the centre due to its own load,

m_e = Mass of beam/shaft to produce unit displacement at the centre, and

a_e   = Amplitude of vibration at the centre.

Because of the definition

         m_e g . y_e = mg

or         m_e y_e = m        ---------- (35)

∴          m_e a_e g = Inertia load on the shaft

For any infinitesimal element 'δx' at distance x, we get the following

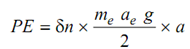
For the whole shaft, the potential energy is specified by

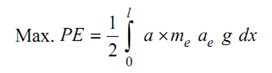                               ---------- (36)

KE of the element

KE = ½ (m δx) (a ω_n )²

Here w_n is basic natural frequency. For the whole shaft, the kinetic energy is specified by

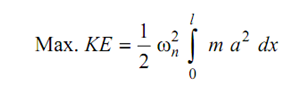
Assume                 y /a = y_e/ a_e = constant (C )

This assumption is constant with practical condition in the manner that the support y = 0 & x = 0 and at the centre y = max and a = max.

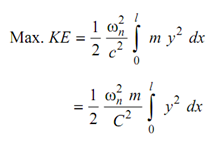               ----------(37)

 Eq. (34) becomes

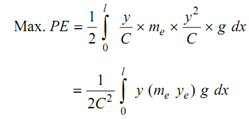
By using Equation (33)

      ------------(38)

 By using Rayleigh's Method and equating these two maximum energies we get

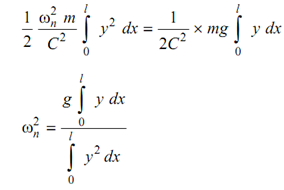----------- (39)