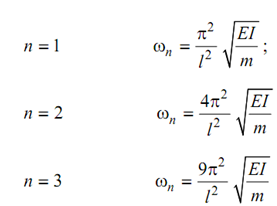Exact Method:
The free body diagram of element of the shaft illustrated in Fig 11 is illustrated here.
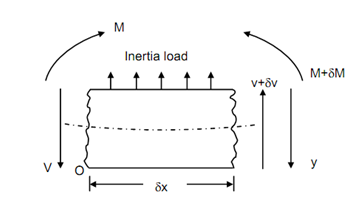
Inertia load = m (∂2 y/∂t2)
(V + δ V ) = V + m(∂2 y/∂t2) δx
or δV/δx = m (∂2 y/∂t2)
or dV/ dx = m (∂2 y/∂t2)
By taking moments around a corner O
(M + δM ) + (V + δV ) δx - M - Inertia load × (δx /2) = 0
By neglecting product of the infinitesimal quantities
∂M/ δx = - V or dM /dx = - V --------- (40)
∴ d 2 M/ dx2 = dV/ dx = - m (∂2 y /∂t 2 )
For beams dy/ dx is negligible.
Since
M/I = E / R or M = EI (d 2 y / dx 2 )
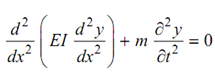-------- (41)
Eq. (41) specified Euler's equation.
For shaft/beams cross-section and material is the similar generally therefore EI will become constant.
∴ EI = d 4 y/ dx4 + m =∂2 y/∂t 2 = 0 -------- (42)
For solving out this equation variable separation method might be used.
Let
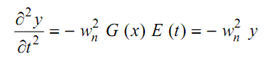
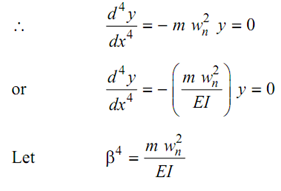
∴ d 4 y/ dx4 = - β4 y = 0 ---------- (43)
The functions that satisfy Equation (43) are cosh β x , cos β x, and sin β x. Hence, the solution may be written as
y = A cos β x + B sin β x + C cosh β x + D sinh β x ------------ (44)
A, B, C and D are constants that can be evaluated using boundary conditions.
For shaft/beam illustrated in Figure 11, the boundary conditions are following
x = 0, y = 0, d 2 y/dx2 = 0
x = l, y = 0, d 2 y/dx2 = 0
By substituting x = 0, y = 0 and d 2 y/dx2 = 0 in Equation (44) we get
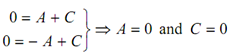
By incorporating the values of A and C in Equation (42) and putting x = l, y = 0 and
d 2 y /dx2 = 0 .
0 = B sin βl + D sinh βl
0 =- β2 B sin βl + β2 D sinh βl
∴ B sin βl = 0 and D sinh βl = 0
If β l is non-zero, sinh β l ≠ 0
∴ D = 0
If B is also zero which will means the shaft/beam is not vibrating. However vibrations are occurring
∴ B ≠ 0 ∴ sin βl = 0
∴ β4 = n 4 π4 /l 4
By substituting for β4, we obtains
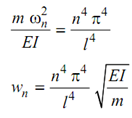-----------(45)
Based on value of n, this will provide infinite natural frequencies equivalent to the infinite modes.
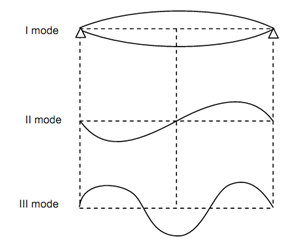
Figure 13
