Common-base Amplifier:

An exemplary common-base amplifier is illustrated in Figure and its small ac equivalent is illustrated in Figure. A routine analysis of the equivalent circuit gives :

                                                      V₀  =- ( g_m V_π ) (R_c || R_L )

Application of KCL at the emitter node gives :

g _m  V _π   + (V_π / r_π )+ (V_π / R_E  )+ V_s  - (- V_π ) /R_S = 0

since β = gm rπ, we can write :

V _π  ((1 +β  / r _π )+ (1/R_E  )+  (1/R_S)) = -V_s/R_s

from where we get

V_π =-      V_s  / R_s  [(r_π  /1 +β )|| R_E  || R_s ]

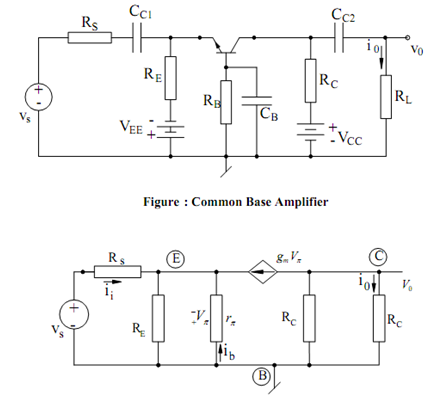
Figure: Small Signal Equivalent Circuit of Common Base Amplifier

The small signal voltage gain of the circuit is, thus, found to be

A_v  = V₀ /V_S = + g_m ((R_c || R_L  )/ R_s) [(r_π/1+β || R_E  || R_s )

as R_s → 0, A_v  ≅ g_m  (R_c || R_L )

The current gain A_i =I₀/I_i may be determined as follows. The KCL equation at the emitter is given by

I _i  + (V_π /r _π )+ g _m   v _π + V_π  /R_E=0

from which we obtain

V _π = - I_i =   (  r_π  /  ( 1+β) || R_E]

The load current is given by

I₀  =- ( g_m V_π ) (R_C  / R_C  + R_L )

Hence,  I₀ /I_i is found to be

A_i  =      I₀  / I_i  = g_m (R_c / Rc + RL) [[ r_π /1 + β)  || R_E ]

In the limiting case, as R_E → ∞ and R_L → 0, then current gain becomes the short circuit current gain specified by

A _i0   = g_m r_π / 1 +β   =  β/1 +β    = α  (as expected)