Hybrid-π Model of a Transistor:

Let each voltage and current be written as the sum of a dc component and a small-signal ac component as follows :

i_C  = I_C  + i_c                 i_B  = I _B  + i_b

v_BE  = V_BE  + v_be          v_CE  = V_CE  + v_ce

If the ac components are adequately small, we can write

 i_c  =  (∂I_C /∂V_BE ) v_be +  ∂IC/∂V_ce ;   i_b =  ∂I_B/∂V_BE v_be

where the derivatives are evaluated at the dc bias values. Three useful small signal parameters of the BJT, known as its trans-conductance g_m, the collector-to-emitter

resistance r₀, and the base-to-emitter resistance r_π, can be defined now as follows :

g_m        =  ∂I_C    / ∂V_BE = I_S /V_T  exp(V_BE /V_T    ) = I_C /V_T       

r_o  = (∂I/          ∂ V_CE )^-1  = [(I_SO /V_A  )exp (V_BE /V_T)]^-1  = (V_A+V_CE/I_C)

r _π  = ( ∂I _B  /∂V_BE ) ^-1     = [ (I_SO / β₀ V_T ) exp (V_BE/ V_T)]^-1     = V_T/I_B

The collector and base currents can, thus, be written as

i _c  = i′_c + (v _ce /r₀  );      i  = v_π / r_π 

where

i_c′ = g_m v_π ; v_π = v_be

The small-signal circuit which models these equations is specified in Figure. It is called the hybrid-π model. The resistor r_x, which does not show in the above equations, is known as the base spreading resistance. It show the resistance of the connection to the base region inside the device. Since the base region is extremely narrow, the connection exhibits a resistance which frequently cannot be neglected.

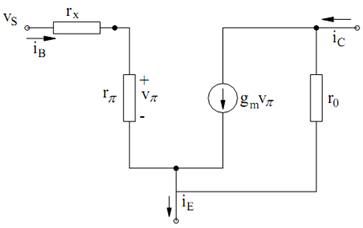
Figure: Hybrid π Model

The small-signal base-to-collector ac current gain β is described as the ratio  i_c′ / i_b. It is given by

β= i_c′ /i_b = g_m v_π /i_b  = g_m   r_π = (I_C  /V_T )( V_T / I_B) = I_C / I_B

Note that ic differs from i′c by the current through r0. Therefore,   i_c/ i_b ≠ β , unless r₀ = ∞.