Hyman Minsky:

A fruitful transition from the short-run dynamics of a macroeconomic model and the real-financial fluctuations associated with Hyman Minsky would be the probe of a benchmark macroeconomic model offered  by him below.

Minsky considers the following equations:  

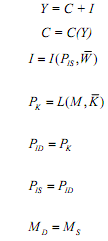
The model is certainly familiar from introductory macroeconomics where the exogenous variable M is money, and the subscripts D and S against it denote demand and supply of money in the money market equilibrium condition. 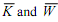 are the given capital stock and wage bill respectively, which are given.  The 'price' of money P_M = 1. PIS is the supply price of a unit of investment, P_K is the market price of existing real capital and  P_ID is the demand price of a unit of investment. The explanatory sequence is as follows: The portfolio balance equation or the liquidity preference relation above yields a value of P_K for every quantity of M. Given W,  I adjusts so that P_IS = P_K. Once I is given, C and Y are determined.

However, productivity of capital takes the form of expected future earnings (gross profits after taxes) of an assembly of capital goods within a producing unit. Recall the arithmetical relation from basic macroeconomics that the value of the capital stock will necessarily equal the discounted value of a stream of future returns. The discussion of the marginal efficiency of capital MEC is relevant here and can be substituted for the equation for P_K. Hence, this one is the unstable equation in the system and shifts downwards whenever a wave of pessimism overcomes investors.

Changes in investors' confidence can lead to potentially destabilising macroeconomic cycles even when the interest rate is relatively stable in the face of aggregate demand shocks. Building upon Keynes, Minsky argued that the explanation for the level of aggregate demand must be sought in the financial markets, in the financing of investment plans. Disequilibria therein affect the valuation of capital assets relative to the price of current output and this price ratio determines investment activity. Keynes'  General Theory, Minsky explained, was concerned with how these two sets of prices (capital and financial assets, on the one hand, and current output and wages, on the other) were determined in different markets by different explanatory variables which gave rise to fluctuations in economic activity.          

In order to understand a modern economy from an appropriate Wall Street perspective rather than through the metaphor of a village fair, the cash flows and related balance sheets of categories of economic agents must be displayed. The flow of funds accounts will depict consistent interlocking asset and liability positions of different classes of receipts and payments. Positions held here determine the flows of goods and services. Balance sheets for a Minsky-type financial instability model are as follows where the details will be found in Lance Taylor's text.

Corporate net worth ?_f is not restricted to be null and emerges as an endogenous variable in the model. Government debt T is held only by the banking system. The money supply rule is, therefore M =  ζT  where  ζ is the money multiplier and the supply of bank loans to firms is L_b = (ζ-1)T. The economy-wide wealth constraint is ,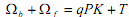 where P_K is the "replacement cost" of the capital stock and q is Tobin's  q. Thus  q_PK would be the asset value of the capital stock.  Given the shares v and λ_h^s  of their wealth ?_h that households hold in the form of equity and loans to firms respectively, their balance sheet identity can be used to scale their net worth to the money supply. Note that rentiers and workers can be distinguished (recall the remarks made in connection with the appraisal of Goodwin) in the equity value P_vV of rentiers. We have

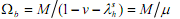
where µ is the share of ?_h held as money. The loan market equilibrium condition is

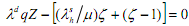
where Z = PK/T is the capital-debt ratio, the state variable.

Minsky suggested that the arguments of the loan demand function λ^d are the interest rate i and the expected profit rate r^e = r + ρ, where r is the observed rate of profit and ρ is an indicator of business confidence. The share of money and loans in household wealth are assumed to depend on the same explanatory variables and u, the capital-output ratio as an indicator of the level of economic activity. The expected profit rate also determines the capital asset valuation ratio  q. The latter is set equal to  r^e capitalized by borrowing costs q = ( r + ρ) / i  When businessmen are optimistic, the investing community ratifies their confidence by increasing its estimates of corporate wealth. From their balance sheet, the net worth of firms 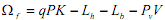follows endogenously from the level of q and loan and equity market clearing. For given levels of ζ and Z, the excess demand for loans (the loan market equilibrium condition above) will be a decreasing function of the interest rate. An increase in  Z  steps up the demand for loans, thereby driving up  i. Conversely, an increase in the supply of loans, a higher ζ, lowers the interest rate.

Potential effects of changes in  ρ or  r on excess loan demand are more interesting. The basic assumption here is that liquidity preference is high in conditions of fundamental uncertainty. During a boom, the speculative demand for money decreases more than the transactions demand goes up. This portfolio switch bids up equity prices Pv in the equilibrium condition of that market

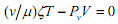
The relative supply of loans goes up. Excess loan demand becomes less sensitive to changes in actual and anticipated profit rates. The slope of the "loan market" curve, or the LM curve so to speak, in the (r,i) plane becomes more shallow at higher levels of r. If investment demand depends on q, then the IS or "commodity market" curve determines macroeconomic equilibrium. A higher level of confidence shifts the LM schedule upward and the IS rightward, leading to a new equilibrium with higher values of r and i. The shift in liquidity preference, however, means that the increase in i relative to r will be greater at a low initial profit rate than at a high one.      

In order to generate an oscillatory response, note that  Z  will evolve over time according to     

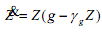
where g is the rate of growth of the capital stock from the IS-LM model and γg is the share of the fiscal deficit in the value of the capital stock. Since a higher value of Z raises the interest rate,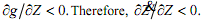 

The other state variable is the state of confidence which, through positive feedbacks, can generate cycles. A higher value leads to an increase in investment and the growth rate. Thus, 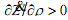Changes in ρ, as well, depend on the state of the economy. For instance, confidence might increase when the actual profit rate  r is high or the interest rate i is low. Thus

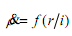
where f is an increasing function.

The two equations above can generate a clockwise cycle. The system is potentially unstable because a higher value of  ρ can make the  i r ratio go up, 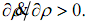. A higher Z raises the interest rate and reduces the level of economic activity and profits. That is,  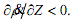A sudden loss of confidence at an initial steady state means that ρ jumps downwards. Consider the stable case when the Jacobian of the system above is positive. The "confidence" schedule,  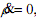, must be steeper than the "velocity" schedule,  . 0 = Z & It continues to decline, with Z also falling because the interest rate is relatively high and  investment is decreasing. After some time, Z may fall far enough to reduce pressure on the loan market and permit the  i r  ratio to rise. When the trajectory crosses the "confidence" schedule,  ρ will begin to rise, finally stimulating growth enough to allow  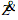. > 0. The upswing might last some time, until the trajectory crosses the flattened "confidence" schedule at high values of Z and  ρ. Depending on the strength of the positive feedback to confidence, the system may oscillate back to the original steady state, orbit it forever, or diverge on a spiral path. 

The swings in confidence might be dampened by the interventions of central banks. Here ρ would be affected by shifting the interest rate through changes in the credit multiplier. However, if the authorities step in to support confidence,  ρ itself may move upward over time leading to increasingly fragile financial positions. Hyman Minsky's cycle moves through the following stages: "Hedge financing" best describes the tranquil period when the anticipated cash flows from operations are adequate to meet future commitments on debts. Over a few such years, confidence and optimism build to generate "speculative financing" wherein the present value of cash flows over a finite horizon are not expected to meet payments commitment. As a run of good years continues, "Ponzi financing" schemes are generated which are outright pyramidal swindles where a subclass of individuals roll over their debt by emitting fresh debt in a never-ending spiral. It is worth observing, as a footnote here, that the standard infinite-horizon optimisation exercise includes the well-known "No Ponzi Games condition" that excludes  these schemes on the grounds of the rationality of borrowers and lenders. At the euphoric peak of the cycle, as both short-term and long-term interest rates drive speculative and Ponzi behaviour, the present values of some Charles Ponzi-type investors will turn negative. Reneging on their commitments will lead to the distress of their lenders who will encash other financial assets. The prices of assets across the board will plummet precipitously impacting on investment plans and profits. While the upper point of the cycle, then, is characterised by a Keynes-type evaporation of the wave of optimism or animal spirits, the lower turning point is a process of debt deflation leading to a stable system with modest hedge funding of projects.