Torsion of Circular Shafts:

Torque is defined as the moment applied about the axis of the shaft. Torsion is the act of applying torque. Because of torsion, twisting of the shaft occurs. Hence, the shear stresses are produced on the cross-section itself.         

A shaft of circular section is said to be in pure torsion while it is subjected to equal and opposite end couples whose axes coincide along the axis of the shaft. In other words, if the moment is applied in a vertical plane about the longitudinal axis of a beam or shaft, will be subjected to a torque causing twist or torsion in the member. As the beam bends because of bending moment, is the angular displacement among two cross-sections of the shaft. Figure illustrated a pulley of radius R subjected to a force W tangential to circumference, after that the

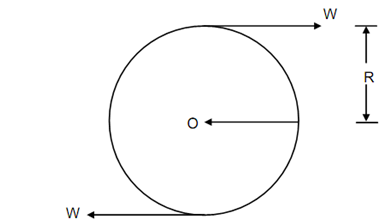
∴          Torque, T = Force × Radius

                            T = W × R

The effect of application of torque on the shaft would be to cause twisting of a section with respect to adjacent section. This action shall result in shearing stress over each section. Figure shows the shearing stress on the element in the direction of rotation which will be accompanied by complementary shearing stress parallel to the axis of the shaft.