Plastic Deformation in Torsion:

We have seen here to calculate the stress at any point on the cross-section of a bar subjected to torque. The maximum stress occurs everywhere on circumference of a circular cross-section. Any material begins to deform plastically if the stress becomes equal to yield strength. In case of a cylindrical shaft the torque that will induce plastic deformation at r = d/ 2 (i.e. on surface) is given by

T_γ = π d ³ τ_γ/ 16

where  τ_γ = Yield strength.

In this situation, yielding is occurring only on the surface but the whole material of the shaft is still elastic. You should be conversant with stress-strain diagram of material. Without much discussion on this diagram, let us assume that material of the shaft has a stress-strain diagram as illustrated in Figure.

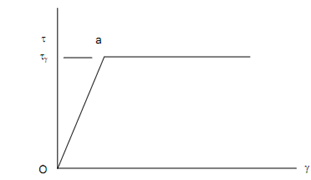
Figure

The material is elastic-plastic which means that once the yielding occurs, further deformation continues at constant stress τ_γ which is shear yield strength of material. This behaviour is very closely demonstrated by low carbon steel for it expands up to 10 times the deformation at yield point (point a in above Figure). Further twisting of the shaft will not cause enhance in stress but the plastic deformation shall spread from outer surface to inside with increasing torque. At last the whole section can be plastically deformed. Figure shows a circular selection of diameter d, deformed plastically up to a radius r _γ . Apparently r _γ  < d/2 .