Hollow Circular Shafts:

It was stated that the hollow circular section shafts can be analysed in the same way as solid shaft with just difference that the polar moment of inertia is computed from Eq. for hollow circular cross-section. The stress at any radius r, i.e. The minimum shearing stress at inner surface shall not be zero but a minimum as shown in Figure (a). For discovering relation among T and τ we may consider the elementary ring like the one in Figure and redrawn for hollow circular section of inner diameter, d_i, and outer diameter, d₀ in Figure. The procedure of discovering force on the ring, and torque around the axis is in essence similar except that the limit of integration shall now be from  di/2 to do /2 , instead from 0 to d .

τ_r / r = τ_m/ (do/2)

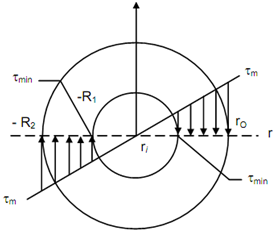
                                 Figure  (a)

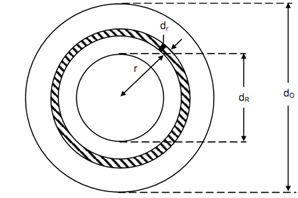
                               Figure (b)

Here τ_m is the stress at any point on the surface where radius is d_o/2

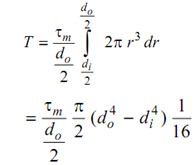
or         T / J h = τm / (do /2)

where

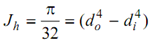
The Eq. are also applicable to hollow circular section if J is replaced by Jh.