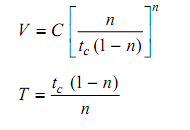Cutting Speed for Minimum Cost

Material removal cost drops with increase of speed, since the machining time is reduced. The piece is machined very rapidly and spends less time on the machine tool. Tool cost increases with cutting speed as the tool wears out much faster at higher speeds, leading to more frequent replacement of the cutting edge.

Non-productive cost such as loading, unloading, gauging and rapid traverse is not affected by spindle speed of machine and hence this cost will remain constant.

If we plot these three costs in a graph and plot the sum of these three costs we can see that at a particular cutting speed the cost is minimum.

For minimum cost, the above equation could be differentiated with respect to cutting speed V, considering the fact that all other conditions such as feed and depth of cut could be maintained constant, we get.

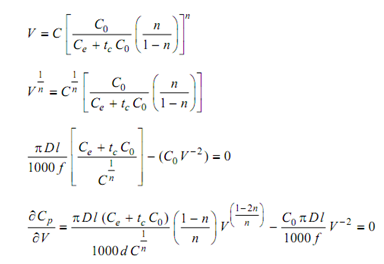
From the tool life equation we can also obtain the minimum cost tool life as

Equation 1

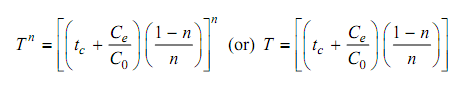
It can also be shown :

Equation 2

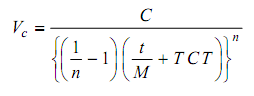
where  V_c = Cutting speed for minimum cost metres/min.,

t = Cost of sharp tool, Rs. per sharp cutting edge,

 M = Machine labour plus overhead rate Rs./min.,

TCT = Tool changing time in minutes (t_c),

n = Slope of tool life vs. velocity curve as plotted in log co-ordinates,  and

C = Taylor's constant for the material.

 From the above expression it can be seen that tool life for minimum cost

Equation 3

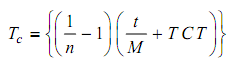
In order to arrive at a maximum production rate we take the total time for the manufacture as

Equation 4

Time = t₁  + t_u1 + t _a  + t₀ /p   + T _m+ ( (T _m t_c ) /T)

For a single pass turning job, it can be shown that

Equation 5

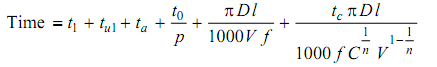
If we now plot these times in a graph and also the sum of these, we find that total time per piece reaches a minimum at a certain cutting speed.

For getting the maximum production rate, the above expression for manufacturing time is to be differentiated w.r.t. cutting speed, V and equated to zero.

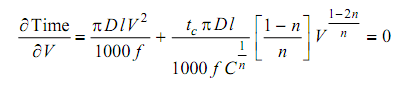
Simplifying, we get

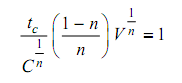
Simplifying, we get