Worst-Case (Arithmetic) Method
The arithmetic tolerance method is the worst-case analysis method. It uses the limits of dimensions to carry out the tolerance calculations. The expected or actual distribution of dimensions is not taken into account. All of the manufactured parts are interchangeable since the maximum values are used. Arithmetic tolerances require greater manufacturing accuracy. It is used when 100 percent interchangeable assembly is required.
Let us assume a closed-loop (the resultant dimension is obtained by adding or subtracting the given dimensions) dimension where set {D} of n element such that the resultant dimension. RD is obtained by adding the first m elements which are called increasing dimensions and subtracting the last (n - m) elements which are called decreasing dimensions. Using this method, all tolerance information about RD is obtained by adding and/or subtracting the corresponding information of the individual dimensions.
Hence we can derive the following:
Nominal dimension = Sum of increasing dimensions - Sum of decreasing dimensions
Equation 2
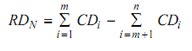
Maximum dimension = Sum of the max increasing dimension - Sum of the minimum decreasing dimension
Equation 3
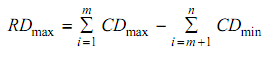
Minimum dimension = Sum of the minimum increasing dimension - Sum of the maximum decreasing dimension
Equation 4
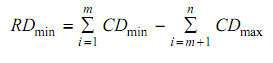
Tolerance on RD :
Equation 5
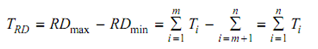
Upper tolerance on RD :
Equation 6
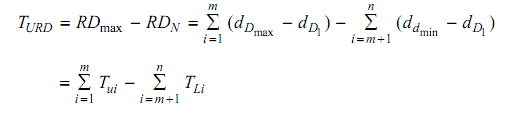
Lower tolerance on F :
Equation 7
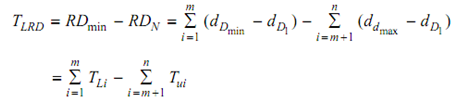
Where Tui and TLi are the upper and lower tolerances on dimension DIN respectively. For unilateral tolerances, one of these variables is zero.