Statistical Tolerancing Method

This method, like the arithmetic method, uses the limits of dimensions to perform tolerance analysis. However, unlike the arithmetic method, it takes into consideration the fact that dimensions of parts of an assembly follow a probabilistic distribution curve. Consequently, the frequency distribution curve of the dimensions of the final assembly follows a probabilistic distribution curve. Typically, the probabilistic distribution curve is assumed to be a normal distribution curve. This method is used in both batch and mass production. It allows for variabilities in manufacturing conditions such as tool wear, machine conditions, random errors, etc. It increases the manufacturing efficiency by increasing tolerance limits and, therefore, reducing the required accuracy of manufacturing.

  Table 4: α and K Values of Typical Distributions

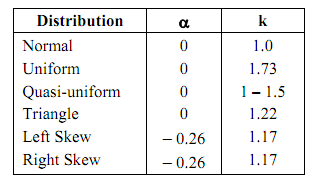
This method is applied to a closed-loop dimension set {D} with each element Di of the set having a probability distribution curve. The design function RD is obtained in the same way as in the arithmetic method. The tolerance information about RD [similar to Equation (2) to (6)] can be obtained statistically as follows. Normal distribution is considered the basis of the analysis. Parameters relating other distributions to the normal distribution are shown in Table 1. The parameters of a distribution curve for one of the elements of the dimension set. When the elements in the dimension set become large enough, the distribution of the RD (the resulting dimension) will be asymptotically normal and independent of the distributions of the individual dimension. Thus we can write:

Equation 8

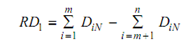
Equation 9

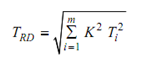
Equation 10

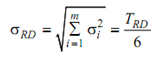
Equation 11

T_LRD =Δ + ( ½) T_RD    

Equation 12               

T_LF =Δ - ½      T_RD                

Equation 13

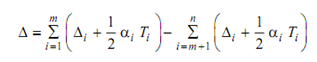
The σ = T_RD/6 used in Eq. (10) is based on assuming a range of 6σ for the distribution curve (3σ on each side of the mean tolerance), Eqs. (11) to

(13) can be viewed as dividing T_RD into upper and lower limits T_URD and T_LRD respectively. If bilateral equal tolerance limits are assumed, then T_URD = 1/2 T_RD and T_LRD = - 1/2 T_RD.