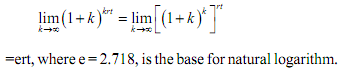Cash flow:

In general, if a principal P is invested at  r percent compound interest for t years, the amount obtained at the end of t years is
notice the difference with the simple interest formula. There , the term within parentheses was 1+rt, that is t is multiplied by r and added to 1. In the case of compound interest, t appears not as a multiplicative term but as an exponent, so that (1+r) is raised to the power t.

We can restate the above by calculating the future value of a single cash flow compounded annually as follows:

Let C₀  be the initial cash flow or investment

r be stated annual rate of interest or return

n be life of investment

C_n  be value of C0  at end of n years.

Then,

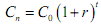
The amount (1+r )^t is called the future value compound factor, denoted FVCF_r,t where the subscripts r and t have the meaning just alluded to. Thus

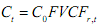
Now we turn to the inverse process, that is, we want to find out, if the future cash flow is of a given amount, what would be the value of the cash flow today. We begin by considering a single period. To convert future cash value into present value, we use the procedure of discounting. To discount a future cash flow to the present, simply rearrange the equation for compounding, to get,

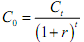
Thus discounting is the opposite of compounding. In the above equation, 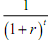is called the present value discount factor PVDFr,t . The discount factor is simply the reciprocal of compound factor. So far, we have considered the case of compounding or discounting a single cash flow. Most financial problems, however, are concerned with multiple cash flows. Let us just take up discounting. Discounting multiple cash flows is simple: we can discount each individual cash flow and then add the present values. The general case is present below (the cash flows are unequal and uneven each year)):

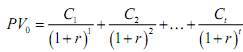
We can now consider the present value of an annuity. An annuity consists of a constant payment received each year. Letting P0
 equal the present value of an annuity which pays C rupees at the end of each year for t years,

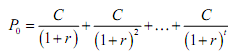
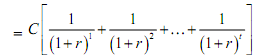
The sequence of terms within the square brackets represents a geometric progression. The geometric progression is called the present value annuity factor (PVAFr,t ) at rate r and t years. Using this notation we can represent the present value of any
annuity as

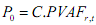
where C is the constant payment amount. It can be shown that the present-value annuity factor can be shown to be equal to

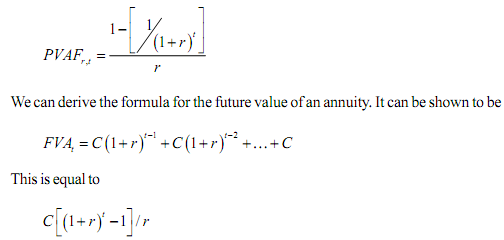
By way of concluding this section let us consider compounding and discounting when cash flow is not on a yearly basis but occurs more than one time a year.

Suppose r is the interest rate, t the number of years, as before, but now suppose it is compounded m times a year, that is, m is the number of compounding periods in a year.

To find out the relevant formula for compounding in such cases, we find it is equal to

Let us ask what happens when compounding takes place not only several times within a year but actually continuously. It may be hard to conceive but is of much use theoretically in economics.

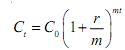
Let  us divide and multiply the exponent by r. we get

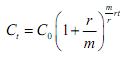
If compounding is done continuously, m will tend to infinity. Writing r/m as k, and knowing that m tends to infinity, so does k , we take the limit of the expression: