Activity Schedule:

Now suppose that each activity, including the critical activities, must be staffed by certain numbers of employees, as shown in the given Table:

Table: Employee Needed for the Project

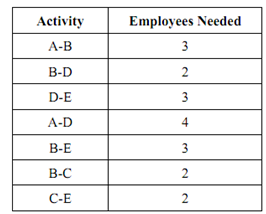
We will now try a few simple scenarios to see the effect that using the slack time in different ways has on the total number of employees needed at any point in the project. Remember that each of the activity can be scheduled individually within the parameters of its free and total slack. Although, to keep things simple, we will try these two scenarios: all of the activities scheduled as early as possible, and all activities scheduled as late as possible. The scenario in which all activities are scheduled as late as possible is illustrated in Figure. The top part of Figure is a Gantt chart, which shows the timing of each of activity as a solid line. For instance, activity A-D starts at time 6 and runs to time 9. The dashed extensions on the A-D line indicate the range of other possible initial times for A-D. The length of the dotted section is the amount of free slack available to the activity. There is no slack for critical path activities. The Gantt chart shows when each activity takes place, and we know how many employees are needed for each activity, thus we may calculate the number of employees needed every day. For instance, between time 8 and time 9 there are four activities taking place simultaneously which are activity B-D (2 employees), activity A-D (4 employees), activity B-E (3 employees) and activity B-C (2 employees) for a total of 11 employees, the peak demand over the entire 16 day period.

Common questions associated to resource levelling include: Will the project complete on time with a limited amount of resource (for example 8 employees)? What is the minimum amount of resource needed to complete this project on time? Given that only a set amount of resource, what is the minimum amount of time in which the project may be completed? Note that this last question takes the resource limit as fixed, and instead permit the project to take more time to complete. As an instance, consider a project in which there is exactly one unit of resource (e.g. one employee) and each of activity requires 1 employee. Now how long will it take to complete the project? The answer is simple: since there is no possibility of doing any of the activities in parallel, the time needed to complete the project is the simple sum of all of the activity durations.