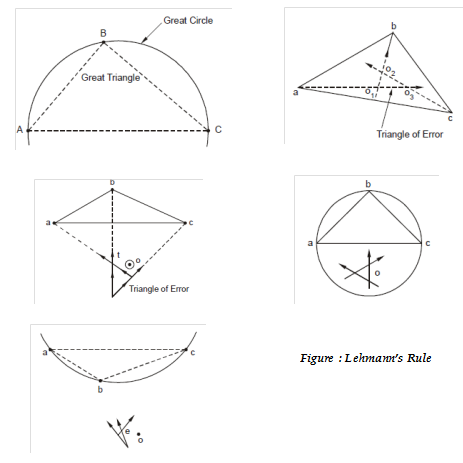
Lehmann's Rule

The Lehmann's rule can be beginning as given below:

(a) The distance of true position of o from every of ray aA, bB and cC is proportional to the distance of O from ground stations A, B and C correspondingly.

(b)  If we look in the directions of stations A, B or C, a true position of station O is on the similar side of the three rays that are aA, bB or cC, i.e. if the table station O is outside the great triangle ABC, the triangle of error will be outside the triangle abc and o will be outside of abc. Same, if table station O is inside the triangle ABC, the triangle of error will be inside abc and o will be inside the triangle of error.

(c)  If the table station O is outside the great triangle other than inside the great circle, the ray to centre station B, bB in Figure (d) lies among the true station position o and intersection of other two rays (i.e. aA and cC).

(d)  While table station is outside the great circle, the table position O in Figure (e) is on the same side of ray towards most distant point (aA) as the intersection of other two rays, 'e'.

Using above rules, the triangle of error is sought to be shrunk to a point fast. The first triangle of error is used to locate new trial position of O (say o1) and placing alidade along o1 and the one of the known point (say a) and then rotating the table so that A is sighted.

Clamping the table within new position, B and C are sighted or rays drawn. A new triangle of error is produced that is much smaller than the first triangle of error. Latest position of table station (say o₂) is marked using Lehmann's rules.

The procedure is repeated until all the rays aA, bB and cC intersect at single point o.