Unbalanced 3 Loads:

An important property of a three-phase balanced system is which the phasor sum of the three line or phase voltages is equal to zero, and the phasor sum of the three line or phase currents is zero.  While the three load impedances are not equal to one another, a phasor sums and the neutral current (I_n) are not zero, and the load is, thus, unbalanced.  The imbalance happens when an open or short circuit appears at the load.

If a three-phase system has an unbalanced load and an unbalanced power source and an methods of fixing the system are complex. Thus, we will only consider an unbalanced load with a balanced power source.

Example: A3 balanced system, as shown in Figure , holds a wye load.  The line-to- line voltage is 240V, and the resistance is 40? in each branch.

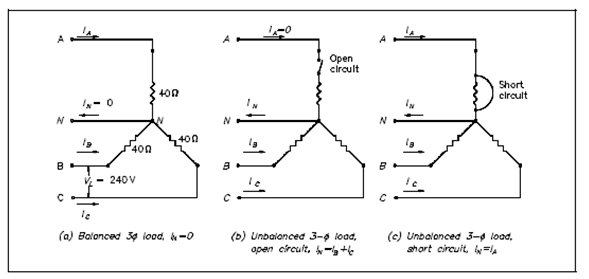
Figure   Unbalanced Load

Find out line current and neutral current for the subsequent load conditions.

1.         balanced load

2.         open circuit phase A (Figure 16b)

3.         short circuit in phase A (Figure 16c)

1.     I_L =I_ø    I_ø = V_ø /R_ø    V_ø  = V_L/√3

I_L =(V_L/√3)/R_ø

=(240/1.73)/40

= 138.7/40

I_L =  3.5 amps  I_N = 0

2.  Current flow in lines B and C becomes the resultant of the loads in B and C connected in series.

I_B = V_L/ R_B +R_C    I_C =I_B

= 240/40+40

I_B = 3 amps     I_C = 3 amps

I_N =I_B+I_C

=3+3

I_N = 6 amps

3.  I_B = V_L/R_B    I_C=I_B

=240/40

I_B = 6amps    I_C = 6 amps

The current in Phase A is equivalent to the neutral line current, I_A  = I_N.  Thus, I_N is the phasor sum of I_B  and I_C.

I_N =√3I_B

=(1.73)(6)

I_N = 10.4 amps

Within a fault condition, the neutral connection in a wye-connected load will carry more current than the phase under a balanced load.  The Unbalanced three-phase circuits are denoted through abnormally high currents in one or more of the phases. This might cause damage to equipment if the imbalance is permitted to continue.