Derive a relation between the torque and shear flow:

We shall now derive a relation between the torque T applied to a hollow member and the shear flow q in its wall. We let a small element of the wall section of length ds illustrated in Figure (a). The area of the elements dA = ds t and the magnitude of the shearing force dF exerted on the element is

dF = τ dA = τ t ds = q ds

The moment dM0 of this force about an arbitrary point o within the cavity of the member may be obtained by multiplying dF by the perpendicular distance p from o to the line of action of dF (Figure (b)).

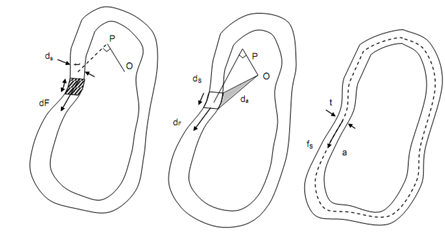
(a)                                   (b)                                       (c)

Figure

We have

dM ₀  = p dF = p (q ds) = q ( p ds)

But the product is equal to twice the area dA of the shaded triangle. Therefore, we get

dM ₀  = q 2dA

Integrating

∫  dM₀  = ∫ q (2 dA)

Here, ∫ dM₀ represents the sum of the moments of all the elementary shearing forces exerted in the wall section, and since this addition is equal to the torque T applied to the hollow member,

T = ∫ dM ₀  = ∫ q (2 dA)

T = 2 qA

where, A is the area bounded by the centre line of the wall cross-section.