Angle of twist of a thin-walled hollows:

The shearing stress τ at any point of the wall may be expressed in terms of the torque T if we substitute for q.

                                         τ=  T / 2 tA

where, t is the wall thickness at the point considered and A, the area bounded by the centre line. For elastic deformation the distribution of stresses across the wall can be assumed uniform, and the above equation shall yield the actual value of the shearing stress at a given point of the wall.

The angle of twist of a thin-walled hollows haft can be obtained by utilizing the method of energy. Strain energy per unit volume

n =( ½)  τ²/  G

Total strain energy of small element of length l and width ds

dU =     (τ²/2G  )dV

∴

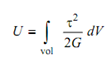
where dV = t l ds and τ from Eq.

∴          U = ∫T2l/ 8 A₂ G . (ds/t)

Since t is variable ( ds /t) is to be integrated. It is better to represent above integral as

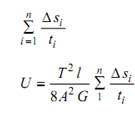
                                                         θ= dU /dT

 ∴  

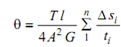
If ds /t is integral, that means. if t may be expressed as function of S, then

θ= (Tl/4 A² G) ∫ds/t