Pressure working on the curved surface:

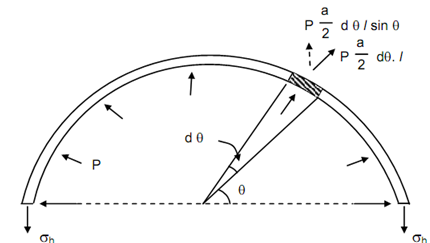
The pressure working on the curved surface acts normal to the surface and therefore, it shall be working in different direction at different points along the surface. The vertical component of bursting force is obtained by considering an element at angle θ to the horizontal that is subtended by an angle dθ at the centre as illustrated in above Figure. The length of this element might be the total length of the cylinder itself. In the vertical direction the revolution of the elemental force is illustrated in Figure.

Figure

The radial force acting on the element,

              p × (d/2) × d θ × l

The vertical component of elemental force,

         p × (d/2 ) × d θ × l sin θ

Therefore, the total vertical component of the bursting force in the top portion of the cylindrical shell shall be

                                               = p . d . l

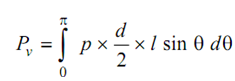
As this resultant vertical component is working upwards, the internal stress on the horizontal strip of dimensions l and t shall be working downwards mentioning that the nature of this stress is tensile.

The resisting force = σ_h  × l × t × 2

As the equilibrium is maintained by the action of bursting & resisting forces only, they should be equal.

                                    σ_h  × l × t × 2 = P d l

                                          σ_h  =  pd /2t

This stress is called as the hoop stress working in the circumferential direction and it shall be tensile in nature.

It may be stated at this stage that the internal stresses in a thin cylindrical shell are working in the longitudinal and circumferential directions and therefore they are named as longitudinal stress and hoop stress and both are tensile in nature. Let us see some instance for determining stresses in thin cylindrical shells.