Expressions for the bursting and resisting forces:
We may write the expressions for the bursting & resisting forces as below.
It may be clearly seen that the bursting force is caused because of the internal pressure working on the vertical circular wall of nominal diameter d.
Hence, the bursting force = p × (π d 2 / 4)
The resisting force is produced by the longitudinal tensile stress σl working on the vertical area exposed, of thickness t and diameter d.
Therefore, the resisting force = σl × π dt
For equilibrium, the resisting force must be equal to the bursting force.
Thus, we get σl × π dt = p ×( π d 2 /4)
Or σl = pd / 4t
This internal stress is called as longitudinal stress, mentioning the direction in which it is working and its nature shall be tensile.
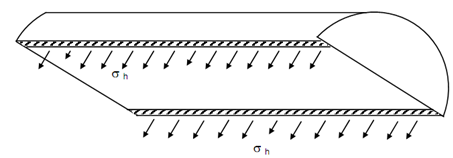
We will now consider a horizontal diametrical plane XX which cuts the cylindrical shell in two halves. The stresses have been illustrated in Figure .
Figure
We shall let the equilibrium of the top portion of the cylinder. The horizontal pressure working on the two end walls shall balance each other and therefore, there will be no longitudinal stress in the wall of the cylinder. The pressure working on the curved surface of the shell makes the bursting force for this free body diagram which must be balanced by the reacting force caused by the development of internal stresses along with wall thickness of the cylinder. As the plane XX is horizontal, the cylinder's wall exposed through the cutting shall also be horizontal and it shall be in the form of two rectangular strips, along longitudinal direction of length l and thickness t. Therefore, the stress working on this strip shall be in the vertical direction.