Stresses:

Figure illustrates a thick cylinder subjected to an internal pressure, P₁ & external pressure P₂. The internal and external radii are respectively r₁ & r₂,.

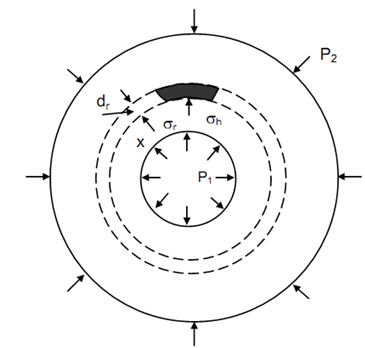
Figure

In order to derive expressions for the internal stresses, let an annular cylinder of radius r and radial thickness dr. On any small element of this ring, σ_r shall be radial stress and σ_h will be the hoop stress. Assuming the equilibrium of the ring similar to a thin cylinder as illustrated in Figure.

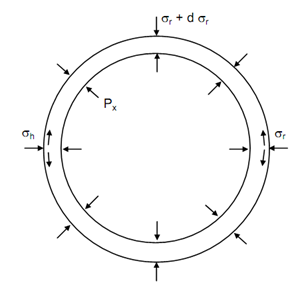
Figure

Through bursting force in the vertical direction, we obtain

 σ_r  × 2 x ×l - [(σ_r  + d σ_r ) × 2 ( x + dr ) × l ]

Neglecting the second order terms,

Bursting force = - 2l (σ_r dx + x d σ_r )

Resisting force = 2 × dr × l × σ_h

Equating the two,        2 × dr ×l × σ_h  = - 2l (σ_r dr + r d σ_r )

σ h  = - σ r  - x (d σ_r/ dr)

Therefore, we get

σ _h + σ _r  +   r d σ_r  / dr  = 0