Thevenin's Theorem and Dependent Sources

Working along dependent sources is different from working along independent sources when applying Thevenin's theorem.

Whereas calculating R_th we can only short circuit voltage sources and open circuit current sources. 

Because the current or voltage of the dependent sources is based upon the current or voltage of these independent sources.

Whilst to calculating R_th we have to short circuit the open terminals of the Thevenin circuit and calculate the I_sc and then divide V_th with I_sc to estimate R_th.

Example:   In the circuit estimate the voltage V_o by Thevenin's theorem.

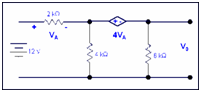
Solution:

                   We will calculate V₀ via Thevenin's theorem .

Step 1:      Remove R_L

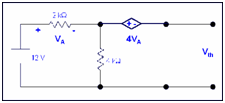
Here R_L is 6k resistor at which we desire to calculate the voltage V_o.

Step 2:  Determining V_th

                                    Voltage of 4k resistor   will be                          

                                                             V_4k = (4k/6k) 12 = 8volts

                                    Voltage across 2k resistor will be

                                                              V_2k= (2k/6k) 12

                                                    V_A = V_2k = 4V

                                                   V_th = 8 - 4V_A

                                                        = 8 - 4(4)

                                                        = 8 - 16 = - 8 volts

Step 3:

While we use dependent sources we will utilize the following technique.

In the above shown circuit output that is opened after eliminating the load resistance we will now replace this open circuit with short circuit. As shown in the circuit below.

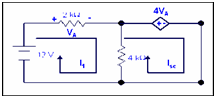
                        First we will discover I_sc to calculate R_th.

                                    Here V_A = 2kI₁

            By applying KVL to loop 1

                                     -12 +2kI₁ +(I₁ - I_sc)4k= 0

                                    -12 +2kI₁ +4kI₁ - 4kI_sc= 0

                                                     6kI₁ -4kI_sc = 12

            For loop 2

                                     (I_sc -I₁)4k +4V_A = 0

                                    4kI_sc -4I₁ +4(2kI₁) =0

                                      4kI_sc -4I₁ +8I₁ =0

                                        I₁ = -I_sc

                        Putting this in equation for loop1

                                                             3I₁ -2I_sc = 6

                                                          3(-I_sc) -2I_sc = 6

                                                         I_sc = - 6/5 mA

            Therefore

                                                 R_th = V_th/I_sc

                                                       =  -8/(-6/5 m) = 6.67k

Step 4:

After estimating V_th & R_th, re-inserting the load resistance R_L in the circuit in series along  R_th and  letting the V_th like a battery in series with these resistances.

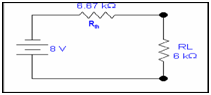
            Therefore

                                                V₀ = (6k/6k +6.67k) x8

                                                                 = 6k/12.67k    x8 = 3.78 V