Q: Evaluate the value of R_L and the highest power dissipation across it through Thevenin's Theorem.

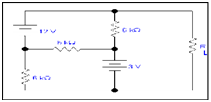
Solution:

We have to calculate R_L and the maximum power across it through Thevenin's theorem

Step 1: Remove R_L

To remove R_L to estimate V_th .In this R_th will be our R_L.

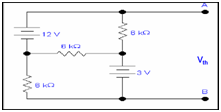
Step 2: Determining value of V_th 

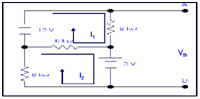
            By apply KVL to the circuit

                                    For path1

                                                 -12 +6I₁ + 6(I₁ - I₂) = 0

                                                            -12 +12I₁ - 6I₂ = 0

                                                                          2I₁ - I₂ = 2 --------------- (i)

                        For path 2

                                                12I₂ - 6I₁ +3 =0

                                                 4I₂ - 2I₁ +1 =0

                                                        2I₁ = 4I₂

                        Put this in equation (i) we get

                                                4kI₂ +1 -1kI₂ =2

                                                            3kI₂ =1

                                                                I₂ = 0.33mA

                        From eq (i)  

                                                                I₁ = (I2 +2)/2

                                                                    = 0.33+2/2 =1.166mA

                        Now voltage of 6k resistor

                                                            V_R6k = 6kI₁

                                                                      = 6k (1.166m) = 7V

                                                            V_th = 3V+7V

                                                            V_th =10 V

Step 3: Estimating value of R_th 

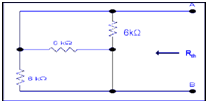
We have to calculate R_th .6k is in parallel along 6k .The resultant is again parallel along third 6k resistor.

                                    6k||6k = (6k x 6k)/6k + 6k = 3k

                                    3k||6k = 6k x 3k/(6k + 3k) = 2k

            Therefore,

                                                         R_th =R_L=  2k

Step 4:  Determining unknown quantity.

After estimating V_th & R_th, re-inserting the load resistance R_L in the circuit in series along R_th and letting the V_th like a battery in series along these resistances.

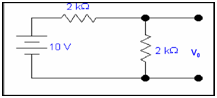
                                                V_RL = 10 x2k/4k = 5 volts

               To evaluate the power dissipation

                                                  P_L = V₂/R = 25/2k

                                                   P_L = 12.5mW