Q:  Determine the current Io by using Thevenin's theorem .

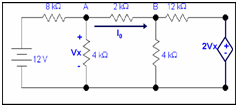
Sol:

We have to calculate I₀ by using Thevenin's theorem .

Step 1:      Remove R_Lto estimate V_th

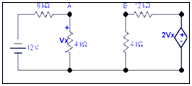
Here R_L is equal to 2k resistor at which we desire to calculate the current Io.

Step 2:  Determining the value of V_th

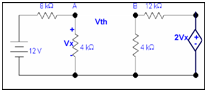
          Now calculate the value of voltage V_th.

                        Voltage across node A

                                                            V_x = (4 x12)/ (4+8) = 4 volts =V_A

                        Voltage across node B

                                                V_B = (8 x V_x) /12+ 4

                                                       = (4 x8) /16                // V_x =4 V

                                                      = 2 volts

                        Therefore

                                                V_AB= 4 -2 = 2 volts = V_th

Step 3:  Determining the value of R_th

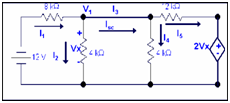
            To determinate the value of I_sc.

                        For node 1

                                     (V₁ - 12)/8k + (V₁ -2V_x)/12k+ V₁/4k +V₁/4k =0

                                                From the circuit          V_x = V₁

                                                (V₁ - 12)/8k + V₁/4k + (V₁ -2V₁)/12k+V₁/4k =0

                                                                   3V₁ -36 +6V₁ +2V₁ +6V₁ -4V₁ =0

                                                                        V₁ = 36/13

                                                I₁ = (12 - V₁)/8k

                                                    =(12 - 36/13)/8k=15/13 mA

                                                I₁ =1.15mA

                                                I₂ = (36/13)/4k = 9/13= 0.692mA

                                                I₄= (36/13)/4 =9/13mA = 0.692mA

                                                I₅ = (36/13 - 2(36/13))/12k =-3/13mA

                                                 I₅= 0.23mA

                                                I₃ = I_sc = I₅ + I₄

                                                    = 0.692 - 0.23

                                                             I₃= 0.46mA

                        Therefore,

                                                R_th = V_th/I_sc

                                                      = 2/0.46m =4.33 k

Step 4: Determining the unknown quantity.

After determining V_th & R_th, re-inserting the load resistance R_L in the circuit in series with R_th and letting the V_th like a battery in series along these two resistances.

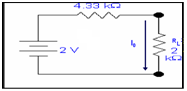
Therefore

                                                I₀  = 2/ (2k + 4.33k) = 0.315mA