Fully Restrained Tapered Bar:

Consider the bar shown in Figure that is circular in cross-section but tapering from a diameter d₂ to d₁ over the length L. The bar is fully restrained at its ends. Presently, let the temperature of the bar increased through ΔT.

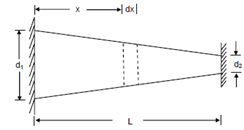
Figure

If the bar were not restrained but free to expand it would have extended through an amount ΔL, given by

ΔL = α L ΔT

Because of the restraint, a compressive force P would have developed within the bar whose effect is to generate a contraction equivalent to ΔL. Under this force, a cross-section at a distance x from the larger end would have established a stress, σ_x, equal to P/A_x, where Ax is the area of that cross-section.

∴          σ_x  = P/A_x = 4P/ π(d₂ +(L-x)/L (d₁-d₂)²)

4P/ π(d₁ -x/L (d₁-d₂)²)

The strain at that cross-section, ε_x, can be written as

ε_x  = σ_x/E  =   4P/Eπ ( d₁ -x/L(d₁ - d₂ ) )²

Under this strain, a small element of the bar of length dx would have changed its length by d (ΔL) given by

d (ΔL) = ε_x dx = 4P dx/πE ( d₁ -x/L (d₁ - d₂ ) )²

The total change in length ΔL can then be obtained by integrating the above expression.

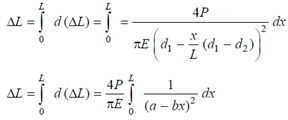
where,  a = d₁ and b =   d₁ -d₂/L

Now, on writing (a - bx) = t, we get dx =- dt/b.

Substituting these,

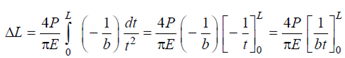
= 4P/ ?bE [1/a-bx]^L₀  = 4P/ ?E [1/d₁-(d₁-d₂/L)x]^L₀ [L/d₁-d₂]

= 4PL/ ?Ed₁d₂

∴ 4PL/?Ed₁d₂ = L α ΔT

So the compressive force generated in the bar due to restraining the free expansion for an increase in temperature ΔT is

P = πE d₁ d₂ α ΔT/4

Hence, the thermal stress, σ_x, at a cross-section with an area of Ax is given as

σ_x  = P/A_x = πE d₁ d₂ α ΔT/4 A_x = E d₁ d₂ α ΔT/(d₁ - x/L(d₁-d₂))²

where x is measured from the end along with diameter d₁ which is the larger end. The maximum stress, σ_max, in the bar occurs at the smaller end along with diameter d₂.

σ_max = E d₁ α ΔT/d₂

For the cross-sections other than circular, the derivation can be preceded in a similar way.