Fully Restrained Tapered Bar:

If the bar were not restrained however free to expand it would have extended by an amount ΔL, specified by

                                      ΔL = α L ΔT

Because of the restraint, a compressive force P would have produced in the bar whose effect is to generate a contraction equivalent to ΔL. Under this force, a cross-section at any distance x from the larger end should have produced a stress, σ_x, equivalent to P/ A_x  of that cross-section. , where A_x is the area of that cross-section

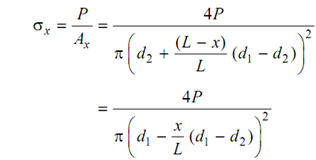
The strain at that cross-section, εx, might be written such as

ε  = σ_x/E  =      4P/ (Eπ (d₁ -(x/L)       (d₁ - d₂ ) )²)

Under this strain, a small element of the bar of length dx would have modified its length by d (ΔL) given by

d (ΔL) = ε_xdx = 4P dx / (πE( d₁ -(x/L) (d₁ - d₂ ) )²)

The entire change in length ΔL can then be get by integrating the above expression.

∴   

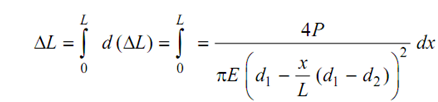
Therefore,

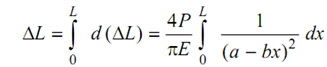
where,  a = d₁ and b = ( d₁- d₂) /L

Now, on writing (a - bx) = t, we obtain dx =- dt / b

Substituting these,

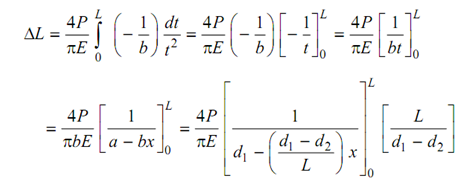
 = 4PL /πE d₁ d₂

          ∴       4PL /πE d₁ d₂= L α ΔT

So the compressive force produced in the bar because of restraining the free expansion for an enhance in temperature ΔT is

P = πE d₁ d₂ α ΔT/4

Therefore, the thermal stress, σ_x, at any cross-section along an area of A_x is specified as

 σ_x  = P/ A_x  = πE d₁ d₂ α ΔT/4 A_x

 = E d1 d2 α ΔT /  (d₁ -(x/L)  (d₁ - d₂ ) ²)

here x is deliberate from the end along diameter d₁ that is the larger end.

The maximum stress, σ_max, in the bar takes place at the smaller end with diameter d₂.

σ_max = E d₁ α ΔT / d₂

For cross-sections other than circular, the derivation might be preceded in a similar kind of way.