Fully Restrained Stepped Bar:

Consider a bar of length L which has a uniform cross-sectional area A₁ over length L₁ although in the rest of the length L2 the cross-sectional area is A₂. Let the Young's Modulus and the coefficient of linear expansion for the two parts be E₁, α1 and E₂, α₂, correspondingly.

The ends of the bar are fully restrained. The bar is display in Figure. Let the temperature of the bar be raised through ΔT.

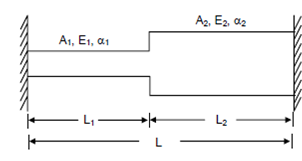
Figure

If the bar were free to expand, it would have extended by a length ΔL given by

ΔL = L₁ α₁ ΔT + L₂ α₂ ΔT

= (L₁ α₁ + L₂ α₂) ΔT

Because the bar is fully restrained, P, the compressive force developed would have to produce a contraction equal to ΔL. Let this force generates a stress σ₁ in part 1 and σ₂ in part 2 (these are the thermal stresses).

σ₁ = P/A₁ , σ₂  = P/A₂

σ₁A₁ = σ₂A₂ or σ₂ =A₁/A₂ × σ₁

σ1 will produce a strain equal to  σ1/E1 and a change in length ΔL₁ equal to σ₁ L₁/E₁

Similarly, σ₂ will produce a change in length ΔL₂ equal to σ₂ L₂/E₂. Thus, the total change in length due to the application of force P will be equal to (ΔL₁ + ΔL₂),

We get,  ΔL₁ + ΔL₂ =     σ₁ L₁/E₁ + σ₂ L₂/E₂

But this should be equal to ΔL.

Therefore, σ₁L₁/E₁ +            σ₂L₂/E₂ = ΔL =( L₁ α₁ + L₂ α₂) ΔT

 σ₂ = A₁/A₂ σ₁

= ΔL = (L₁ α₁ + L₂ α₂) ΔT

∴ σ = (L₁/E₁ +L₂A₁/A₂E₂) = ΔT (L₁ α₁ +L₂ α₂)

Hence   ∴ σ₁ = ΔT E₁ E₂ A₂ (L₁ α₁ +L₂ α₂)/(A₁E₁L₂ +A₂E₂L₁), and

∴ σ₂ = ΔT E₁ E₂ A₁ (L₁ α₁ +L₂ α₂)/(A₁E₁L₂ +A₂E₂L₁).