Fully Restrained Stepped Bar:

If the bar were free to expand, it would have extended by a length ΔL given by

ΔL = L₁ α₁ ΔT + L₂ α₂ ΔT

= (L₁ α₁ + L₂ α₂) ΔT

Since the bar is fully restrained, P, the compressive force produced would have to produce a contraction equal to ΔL. Consider this force generate a stress σ₁ in part 1 and σ₂ in part 2 (these are the thermal stresses).

σ₁ = P/A₁  , σ₂  = P/ A₂

σ ₁A₁  =σ ₂ A₂ or σ  = A₁/A₂  × σ₁

σ₁ shall produce a strain equal to   σ_1/ E₁ and a change in length ΔL1 equal to   σ₁ L₁ / E₁

Likewise, σ₂ shall produce a change in length ΔL₂ equal to   σ₂ L₂/ E₂ . Therefore, the total change in length due to the application of force P will be equal to (ΔL₁ + ΔL₂  ) ,

We get,

ΔL₁ + ΔL₂ =     σ ₁L ₁ / E₁   +     σ ₂L₂/ E₂

But this should be equal to ΔL.

Therefore,          σ ₁L₁ / E₁ + σ₂ L₂/ E₂  = ΔL = (L₁ α₁ + L₂ α₂ ) ΔT

But,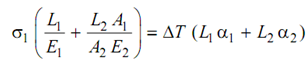

σ₂  =   ( A₁ / A₂) σ₁

∴          σ₁ ((L₁ /  E₁)   +  (L₂A₁)/(A2E2) = ΔT (L1 α1 + L2 α2 )

Hence,

∴          σ ₁ = (ΔT E ₁E  ₂A₂(L₁ α ₁ + L  ₂α ₂))/ ( A₁ E₁ L₂  + A₂ E₂ L₁ )

     ∴         σ ₂ =    (ΔT E ₁E  ₂A₂(L₁ α ₁ + L  ₂α ₂))/ ( A₁ E₁ L₂  + A₂ E₂ L₁ )

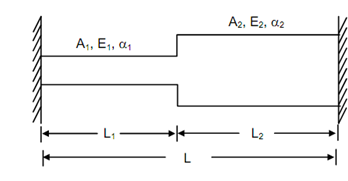
                                    Figure

Herein, we have assumed that the two parts of the bar are build of two different materials. Rather, if the total bar is of a single material of Young's Modulus E and coefficient of linear expansion α,

E₁ = E₂ = E and α₁ = α₂ = α

Then σ₁ and σ₂ decrease to

σ₁ = (ΔT E A₂ α L ) / (A₁ L₂  + A₂ L₁)

σ₂  =  ΔT E A α L / (A₁ L₂  + A₂ L₁)

Furthermore, if the cross-section is uniform throughout (A₁ = A₂ = A), both the above expressions decrease to

σ₁  = σ₂  =σ = E α ΔT

a result which we have already derived for uniform bars.