Calculate the thermal stress in the bar:

A stepped bar made of aluminum is held among two supports. The bar is 900 mm in length at 38ºC, 600 mm of which is with a diameter of 50 mm, when the rest is of 25 mm diameter. Calculate the thermal stress in the bar at a temperature of 21ºC, if

(a)  the supports are unyielding, and

(b) While the supports move to each other by 0.1 mm.

Given  E for aluminum = 74 kN/mm²

               α for aluminum = 23.4 × 10^-6 K^-1

Solution

While the Supports are Unyielding

We have, L₁ = 600 mm; diameter d₁ = 50 mm

Therefore,        A₁ = π(50) ²/4  mm²

Also,    L₂ = 300 mm; diameter d₂ = 25 mm

Therefore, A₂ = (π(25) ² )/4 mm²

and      ΔT = 38 - 21 = 17ºC

Thus, free contraction, ΔL = L α ΔT = 900 × 23.4 × 10- 6 × 17 = 0.358 mm.

Assume σ₁ be the stress in 50 mm φ part and σ₂ be the stress in 25 mm φ part.

Then,  

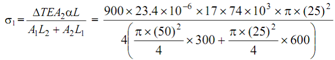
= 14.72 N/mm²

σ₂ = σ₁   A₁/A₂    = 14.72 ×(50)²/(25)²

   = 58.88 N/mm²

 These stresses are tensile in nature.

While the Supports Move to Each Other by 0.1 mm

Here,  ΔL´ = 0.1 mm.

 ∴      

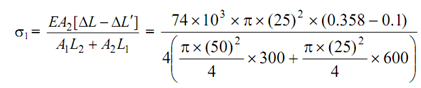
                              = 10.61 N/mm²

∴          σ₂ = 10.61 × (50) ²/(25) ² = 42.44 N/mm²

Both these stresses are tensile.