Forces working on the compound bar for equilibrium:

Though, as the two materials are rigidly joined since a compound bar & subjected to the similar temperature rise, each material shall attempt to expand to its free length position but each shall be affected by the movement of the other. The higher coefficient of expansion material shall effort to pull the lower expansion material to its free length, but shall be held back by the latter to its own free length location. In practice, a compromise shall be attained with both extending to a general position in between the specific free length location. It, in effect, is equivalent to a contraction in bar 2 from its free length location and an expansion of bar 1 from its free location. Therefore, the higher coefficient of expansion material produced tensile stresses, while the temperature of the compound bar enhance. It shall be vice-versa while the temperature decreases. From Figures (c) to (f), it is apparent that

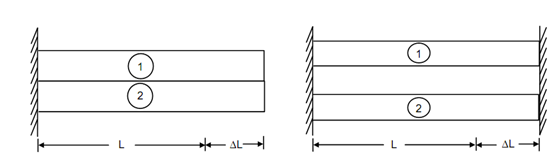
Extension of bar 1 + Contraction of bar 2 = Difference in free lengths

Let the stresses in bars 1 and 2 be σ₁ and σ₂ because of the temperature change. Then the above rule might be written as

σ₁L /E₁ + σ₂ L/E₂ = (α ₂- α ₁) L ΔT

 As there are no external forces working on the compound bar, for equilibrium, the compressive force in bar 2 must be equal to the tensile force in bar 1. It means that

σ₁ A₁ = σ₂ A₂

From the above two expressions, σ1 and σ2 can be written as

σ = A₂ E₁ E₂ (α₂ - α₁) ΔT/ (A₁ E₁ + A₂ E₂)

and

σ  = A₁ E₁ E₂ (α ₂ -α ₁) ΔT/ A₁ E₁ + A₂ E₂

The extension of the compound bar, i.e. ΔL is given as

ΔL = L α  ΔT + (α₁ / E₁) L

ΔL = L α₁ ΔT + A₂ E₂  (α₂  - α₁ ) L ΔT/( A₁ E₁ + A₂ E₂)

ΔL = ( A₁ E₁ α₁ + A₂ E₂ α₂ ) L ΔT/( A₁ E₁ + A₂ E₂)