Calculate the final stresses in the bolt:

A steel bolt of diameter 12 mm & length 175 mm is utilized to clamp a brass sleeve of length 150 mm to a rigid base plate as in given figure. The sleeve contains an internal diameter of 25 mm & a wall thickness of 3 mm. The thickness of the base plate is 25 mm. Initially, the nut is tightened till there is tensile force of 5 kN in the bolt. Now the temperature is grow up by 100°C. Calculate the final stresses in the bolt and the sleeve.

For computation reason, take following values :

E_b = 105 GNm^-2 ; E_s = 210 GNm^-2

α_b = 20 × 10 ^-6 K^-1 ; α_s = 12 × 10 ^-6 K^-1

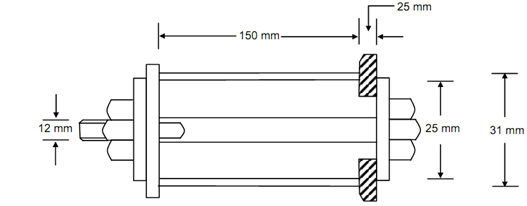
        Figure

Solution

Assume the free thermal expansions of steel & brass is Δs & Δb & Δ is the common expansion. So

Δs = (175) (12 × 10^-6) (100) = 0.21 mm

Δb = (150) (22 × 10^-6) (100) = 0.3 mm

If the first stresses in steel & brass because of 5 kN load are σ_s1 & σ_b1, So

 σ_s1 = + (5 × 10³ × 4) / (π (12)²) = + 44.21 N/mm²          (Tensile)

σ_b1 = -(5 × 10³ × 4 )/ π (31²  - 25 ²)

            = - 18.95 N/mm (Compressive)

Equilibrium of thermal stresses σ_s2 and σ_b2 needs that

σ_{s 2} × (π (12)² /4) + σ_{b 2} × π (312  - 252 )/ 4 = 0

or         3 σ_s2 + 7 σ_b2 = 0

The thermal strains are specified by

ε _s = (Δ- Δs )/ 175

&

ε _b  = (Δ- Δ_b )/ 150

Therefore, the thermal stresses are as:

σ_s2= (210 /175) (Δ - Δ_s) × 10³ N/mm²

 and

σ _{b 2} = (105/150 ) (Δ - Δ _b) × 10³  N/mm²

By substituting these in the equilibrium equation,

3 × (210/175 ) (Δ - 0.21) × 10³  + 7 × (105/150) (Δ - 0.30) × 10³  = 0

Hence, Δ = 0.262 mm

Therefore,

 σ_s2  = (210 /175) (0.262 - 0.21) × 10³  = + 62.26 N/mm²          (Tensile)

σ _{b 2}      = (105 /150 )(0.262 - 0.3) × 10³  = - 26.28 N/mm²          (Compressive)

Total stresses are therefore as follows :

σ_s = σ_s1 + σ_s2 = - 106.5 N/mm²           (Tensile)

σ_b = σ_b1 + σ_b2 = - 4.56 N/mm²            (Compressive)