Shearing Stress:

A thin ring of depth dr at a radius r is chosen on the cross-section as illustrated in Figure. At this radius shearing stress τ_r acts on the ring, whose area is following

dA = 2π r . dr

Thus, the shearing force on this ring,

Fs  = τr  dA

or         F  = r .  τ _m /(d/2) . 2π r dr d

The torque because of  this shearing force is

dT = Fs . r = (4π τm /d) . r³ dr d

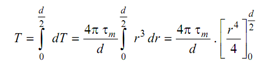
or,

 T = τ_m/(d/2) . π d⁴/32

 In the above equation, π d ⁴ /32 is the polar moment of inertia of circular section of diameter, d and is mention by J.

Hence,

T / J = τ_m/(d/2)

Using Eq. (7), we can write

τ_r / r = T / J  = Gθ/ l

Above are the torsional relationships - three equations correlating :

T = Torque on circular cross-section shaft,

J =  (π /32 )d ⁴ = Polar moment of inertia of circle of diameter, d,

θ = Angle of twist in radians,

G = Modulus of rigidity,

L = Length of the shaft, and

τ_r = Shearing stress at a point on circular section at radius, r. The polar moment of inertia is defined as

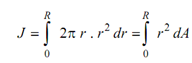
 J represents the moment of inertia of the shaft section around the axis of the shaft. The moment of inertia of a plane area, w.r.t. an axis perpendicular to the plane of the figure is called as polar moment of inertia with respect to the axis normal to the plane. In a circular plane, always the z-axis is through the centre of the circle. Thus, J is known as polar moment of inertia that means moment of inertia about z-axis.