Hooke law:

Hence,

γ _r  = r . Δ θ/ Δ l

However γ_r remains constant for any given value of r, hence, Δ θ /Δ l should also be a constant. This means that the ratio of angle of twist and length of shaft is a constant, that means and θ / l is constant

                                                Δθ / Δ l = θ/ l

Hence,

γ_r  = r . θ/ l

Since Hooke's law is followed  γ_r  =    τ_r /G

where τ_r is the shearing stress at any point on a circle of radius r as γ_r  is the shearing strain at the same point. G is modulus of rigidity of the shaft material. Using this value of γ_r  in Eq. and obtaining

τ_r / r = Gθ / l

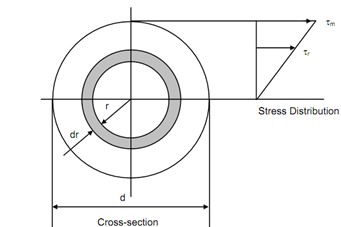
The right hand side of Eq. is a constant for a given length of shaft under a given torque T. Thus, this equation states that ratio of stress at a point to radial distance of that point from the centre of the cross-section is constant. If the shearing stress at any particular point is d/2 called τ_m, the radial distance of that point from the centre of the cross-section shall be and hence,

                        τ_r  / r = τ_m/(d/2) = Gθ /l

or,                     τ_m = Gθ/  l

Apparently the distribution of shearing stress is given by the equation τ_r  = r  (Gθ/l) which shows τ_r is uniformly distributed with radius r. The values of τ_r = 0 at r = 0, i.e. at centre and the shearing stress will be maximum while r = d , i.e. on the surface of the shaft.

Thus, τ_m is the highest value of stress caused by torque T. The distribution of shearing stress over shaft cross-section is shown in Figure.

Figure