Moment Distribution:

The moment distribution technique is a extremely convenient and useful method for finding the bending moment in a rigid jointed structure, like portal fames and continuous beams.

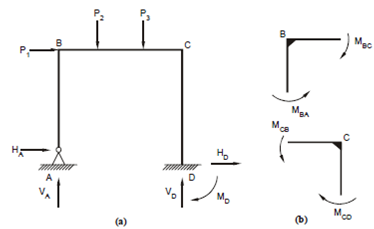
Figure: A Portal Frame

Figure 1 shows a portal frame with vertical members (column members) AB and CD and the horizontal member (beam member) BC which is rigidly joined at B and C so that the angles between the members remain fixed (in Figure 1 these are a right angles). Since the joints B and C are not hinged, but fixed therefore, bending moments will appear both in members BA and BC at joint B and similarly in CB and CD at joint C. In Figure 1(b) we have the conditions of static equilibrium at the joints stating that the sum of all the moments acting at the joint must be zero.

i.e.       M_BA + M_BC = 0

and     M_CB + M_CD = 0

However, the moments themselves are unknowns and can be termed as internal redundants. Also the portal may be supported in any manner. Here, in Figure 1, the support A is a hinge where two reactions (V_A and H_A) are present, while the support D is fixed causing three reactions V_D, H_D and M_D there. Thus, the portal has five unknown support reactions and we have only three equations of static equilibrium to determine them. Thus, externally also it is indeterminate to the second degree (5 - 3 = 2). To solve them by compatibility method will involve a solution of so many simultaneous equations which is a laborious process.