Vibrations of Diatomic Molecules:

A vibrating diatomic molecule, AB can be visualised as a simple harmonic oscillator in Figure. The two atoms A and B (shown as balls) are assumed to be joined by a bond (shown as a spring) of length r_eq and molecule is oscillating around its mean position, r_eq.

The quantised energy levels obtained by the quantum mechanical treatment of the harmonic oscillator are given in Figure (a). A higher energy corresponds to larger amplitude of oscillation. A harmonic oscillator model of a diatomic molecule however, is oversimplified and has some limitations. For example, such a molecule would never dissociate no matter how much of the energy we provide. More and more energy would just increase the amplitude of vibration. This, as you know, is in contradiction with the actual situation as the real molecules do dissociate. The real molecules are not like harmonic oscillators; these have some element of anharmonicity. While we consider the anharmonic nature of the vibrating diatomic molecule, the energy levels get modified as shown in Figure (b).

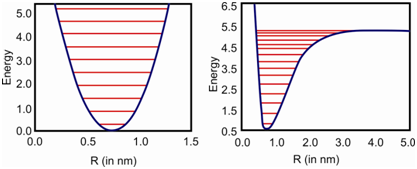
(a)                                                                    (b)

Figure: The potential energy curves for a) harmonic and b) anharmonic oscillator