Dynamic games of complete but imperfect information:

Games are called to be of imperfect information if at least at one node of the extensive form representation, the player with the move  does  not  know  the full history  of  the  game. Before we  discuss the dynamic  games  of  complete  and perfect information,  we would define  the concept of sub-game perfect Nash equilibrium. Sub-game perfection  is  a refinement of the concept of Nash equilibrium.  

Sub-game Perfection:

Example:

We  extend  Example  12  to  illustrate  the  idea  of  sub-game perfect Nash equilibrium. We retain the description of the first stage of the game. But  in the second  stage both  Coke and Pepsi  take simultaneous decision whether  to be tough  or  accommodating.  We  describe the game  and  the payoffs  in  the following game tree.

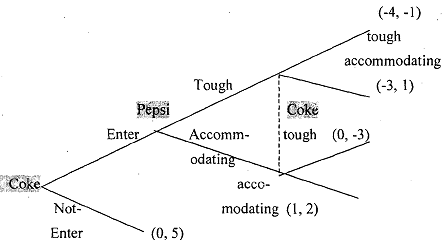
Clearly, in situations like above we cannot solve the game inducing method of backward induction. As the information set of Coke  in the second stage  is not singleton. As the information set in the second stage is not singleton for Coke, it  is  a  game  of imperfect information, that  is,  Coke  does  not  know what decision  has  been  taken  by  Pepsi  in  the  same  stage.  1'n  such  a situation, we introduce  the concept of  sub-game  perfection. But  before  defining sub-game perfection Nash equilibrium, we must know what a sub-game is.

Definition: A sub-game  is a  part  of the game, which  starts  from  a singleton information set and stretches up to the end of the game.

A sub-game must satisfy  the following:

a)  Begins at &singleton  information set.

b)  Includes all the decision and terminal nodes following the  initial node in the game tree (but no node, which does not follow the initial node).

c)  It does not cut any information set.

d)  A game is itself a sub-game ofits own (trivially).

e)  All  the sub-games of  a game except  the game  itself  are called proper sub-games.