Portfolio Theory:

Markowitz's work on portfolio theory considers how an optimizing investor would behave. This theory asserts that in constructing a portfolio of assets, investors seek to maximize the expected return from their investment given some level of risk they are willing take. Those portfolios that satisfy this requirement are called efficient portfolios. Markowitz's theory explains how this should be done.

Markowitz made certain assumptions regarding the behaviour of investors. These are as follows:

1) Investors choose portfolios on the basis of their expected mean and variance of return.

2) Investors are risk-averse expected utility maximisers

3) Investors have a single-period time horizon, and it is the same for all investors.

4) Investors have identical expectations about expected returns, variances, and covariances for all risky assets.

Basically, Markowitz suggested the following procedure for choosing optimal portfolio of risky assets: mark out the set of efficient portfolio; specify the return-risk indifference curves; and choose the optimal portfolio. This is elaborated below. The first thing to do is visualise a diagram where expected returns are depicted on the vertical axis and risk (variance on the horizontal axis:

Now the thing to notice is that if we drew indifference curves on this space, (the thing on the horizontal axis is a 'bad' (a 'bad' is  something the more you consume of, the less utility you get-like pollution. Here risk is a 'bad'). Thus if we were to draw indifference curves on the return-risk space, they will be convex -but upward sloping! They would look like the following:

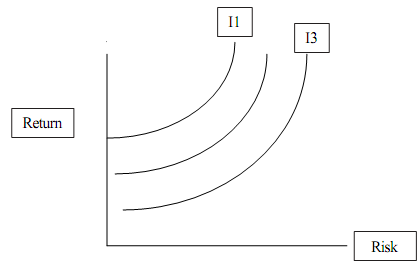
All points on an indifference curve provides the same level of satisfaction. The steeper the slope of the indifference curve, the  greater the degree of risk aversion. As one moves  leftward across different indifference curves, the utility increases. Indifference curve I1 gives a higher level of satisfaction than indifference curve I3. Now let us see how the set of efficient portfolio (what is called the efficient frontier) is delineated. Given the same level of risk, different portfolios will have different returns. The investor will select the portfolio with the with the greatest expected return for a given level of risk. Usually the procedure for obtaining the highest expected return for a given level of risk is found by using a complicated mathematical technique called quadratic  programming, which is an optimisation technique. It is beyond the scope of our discussion. We can give an intuitive explanation.

Given the assets that are available, an investor can create many possible portfolios. Any portfolio that can be created from the available assets is called a feasible portfolio.

The collection of all feasible portfolios is called the feasible set of portfolios.  However only a subset of the frontier of the feasible set of portfolios will be the Markowitz efficient set of portfolios. Finally to choose a single portfolio, the investor will choose that point on the return-risk space where the Markowitz efficient set of portfolios is tangent to an indifference curve. This is the optimal  portfolio.