Proofs of Theorems:

Theorem I

Consider AB be a curve in a vertical plane passing through the vertical axis z as illustrated in Figure. The x and y axes are in the horizontal plane. Rotate the curve around z-axis still it is in ZOX plane.

Assume L be the length of the curve AB. Consider a small elemental length PQ = (δ L) on this curve as illustrated in Figure. If the curve AB is rotated around z axis through an angle θ, the surface S produced by it is illustrated as AA′ B′ B.

Element PQ shall generate a surface PP′Q′ Q specified by

 (δ S) =  PQ × PP′  = δ L × x θ

Here, θ is common angle of rotation for any element on AB.

∴          Total surface

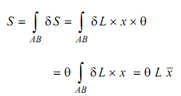
 Here, x  is the x coordinate of the centroid G of the length AB.

∴ S =  L × ( x¯ θ)

= Product of L and the distance ( x¯ θ) travelled by the centroid G throughout the rotation through ∠ θ around the axis of rotation.